Chapter 10 Appendix 10-1
Other Topics in Standard Costing
James R. Martin, Ph.D., CMA
Professor Emeritus, University of South Florida
Chapter 10 | MAAW's Textbook Table of Contents
Standard Process Costing | Material Mix and Yield Variances
| Alternative Analysis for Fixed Overhead
The illustrations in the previous sections of this chapter are general in the sense that a cost flow assumption is not explicitly mentioned. Look back at any of the examples and you will find that the number of units produced is always given and there is no mention of an ending inventory of work in process, or the need to calculate equivalent units. This is a simplification that makes it easier to introduce the standard cost accounting techniques, but it is not very realistic. Once you understand the basic standard cost system presented in the first part of this chapter, you will be ready to add an ending inventory of work in process. Thus, you might want to work one or two basic problems first before you plunge into this section.
The Standard Process Costing Difference
In standard process costing, the standard quantity allowed is based on the equivalent work performed during the period. The units produced during the period are equal to the equivalent units produced. Remember from Chapter 5 that this includes any work performed on the units that remain in the ending inventory of work in process. You may remember how to calculate this from Chapter 5. To refresh your memory the calculation is as follows:
Equivalent Work Done During the period stated in Equivalent Units = Units Completed - Equivalent Units in BWIP + Equivalent Units in EWIP
This equation represents the denominator of the unit cost calculation (Chapter 5, Equation 7) when the FIFO cost flow assumption is used in historical process costing. It is also appropriate in standard process costing because it provides the needed measure of the work performed during the period, excluding any work done to the units in beginning work in process during the previous period. This quantity provides the basis for determining the standard cost allowed. The equivalent units produced are treated just like the units produced in the simplified problems presented earlier in this chapter to calculate the standard quantities allowed. Therefore, the only difference between standard process cost problems and general standard cost problems is that the equivalent units must be calculated first before the standard quantities allowed can be calculated. Also remember that the stage of completion for materials and conversion is usually different. This means that at least two equivalent unit calculations will be needed. Two additional points deserve emphasis. The FIFO cost flow assumption is always appropriate when determining the equivalent work performed in a standard process cost system, and actual unit costs do not need to be calculated. Why? Because the costs flow through the accounts at standard cost.
Material Mix and Yield Variances
There are a variety of possible extensions to the basic variance analysis presented in this chapter. Although it is not practical to include all possible variations of variance analysis, one or two additional types of analysis will provide you with a feel for the variations of variance analysis found in practice. Material mix and yield variances provide a variance analysis extension that some firms have found useful.
When different types of materials may be used as substitutes for each other, a standard mix is usually determined to insure a quality product at the lowest possible cost. If the actual material mix varies from the standard mix, both quality and cost may be affected. The effect on cost can be determined by separating the material quantity variance into two variances referred to as material mix and material yield variances. In addition to the substitutability requirement, the unit of measure for the various materials needs to be the same. Materials may be measured in gallons or pounds or board feet, or some other measure, but the unit of measure must be the same for each ingredient. If these two prerequisites are satisfied, material mix and yield variances can be calculated.
The technique involves two steps. First, the actual quantities of material used are adjusted to the quantities that would have been used if actual materials usage had conformed to the standard mix rather than some other mix. This calculation for each type of material is as follows:
AQA = (Total Material inputs)(Standard Mix Ratio)
where: AQA = Actual quantity of material adjusted to the standard mix.
The actual quantities adjusted represent the quantities that would have been used if the same total quantity had been placed in production, but in proportion to the budgeted mix ratios for each product. After the AQA values have been determined, then the material mix and yield variances are calculated in the following manner which separates the material quantity variance into two parts.
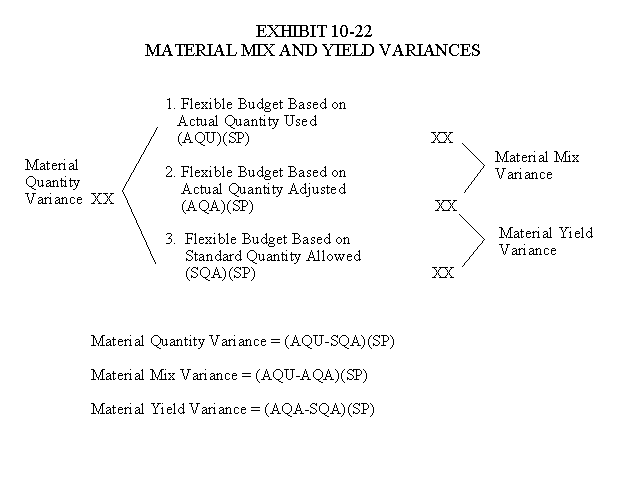
Material Quantity Variance = (AQU - SQA)(SP)
Material Mix Variance = (AQU - AQA)(SP)
Material Yield Variance = (AQA - SQA)(SP)
Conceptually there are three flexible budgets involved in these calculations as illustrated in Exhibit 10-22.

The material quantity variance is the difference between a flexible budget based on the actual quantity used and a flexible budget based on the standard quantity allowed. To separate the material quantity variance into mix and yield variances, we simply place a third flexible budget based on the actual quantities adjusted between the other two as illustrated in the diagram above.
Although the variance calculations are straight forward, there is one confusing aspect about this type of variance analysis. In production processes that involve mixtures of several ingredients, (particularly liquids) lost units are fairly common. For this reason, a standard yield is usually stated as a proportion of output per input. The confusing part is how to determine the standard inputs per output. If standard inputs per output are not given, they may be calculated in the following manner:
Standard Quantity of Input Allowed Per Output = Standard Input Quantity of Each Material in a Standard Batch ÷ (Total Standard Inputs in the Batch)(Standard Yield Ratio)
An example will help clarify the techniques and concepts involved.
EXAMPLE 10-5
Assume Texas Burger Company combines three ingredients in the production of the firm's popular hamburger. The standard quantities and input prices of these materials are provided below for a normal production batch of 2,000 pounds.
| Material | Standard Mix | Standard Inputs lbs | Standard Price |
| Secret A | 10% | 200 | $1.00 |
| Beef | 50% | 1,000 | 2.00 |
| Secret B | 40% | 800 | 1.50 |
| Total | 2,000 |
The standard yield is 90 percent. This means that 1,800 pounds of output (.9 multiplied by 2,000) is expected from 2,000 pounds of input.
The following data are provided for a recent production period in which 21,800 pounds of materials were used to produce 19,350 pounds of hamburger.
| Material | Actual Quantities Used lbs |
| Secret A | 2,000 |
| Beef | 11,100 |
| Secret B | 8,700 |
| Total | 21,800 |
The requirements are simply to calculate the materials quantity, mix and yield variances for this situation.
The Standard Quantities of Input per pound of Output are:
Secret A = 200/1,800 = 2/18
Beef = 1,000/1,800 = 10/18
Secret B = 800/1,800 = 8/18
To avoid rounding errors, the fractions are used in the calculations below.
The Standard Quantities of inputs Allowed (SQA) are:
Secret A = (2/18)(19,350) = 2,150
Beef = (10/18)(19,350) = 10,750
Secret B = (8/18)(19,350) = 8,600
The Actual Quantities Adjusted to the standard mix (AQA) are:
Secret A = (.10)(21,800) = 2,180
Beef = (.50)(21,800) = 10,900
Secret B = (.40)(21,800) = 8,720
Finally, the variances are calculated in the following manner:
| Material Quantity Variance = (AQU - SQA)(SP) | |
| Secret A = (2,000 - 2,150)(1) = | $150 F |
| Beef = (11,100 - 10,750)(2) = | 700 U |
| Secret B = (8,700 - 8,600)(1.50) = | 150 U |
| Total | $700 U |
| Material Mix Variance = (AQU - AQA)(SP) | |
| Secret A (2,000 - 2,180)(1) = | $180 F |
| Beef (11,100 - 10,900)(2) = | 400 U |
| Secret B (8,700 - 8,720)(1.50) = | 30 F |
| Total | $190 U |
| Material Yield Variance = (AQA - SQA)(SP) | |
| Secret A (2,180 - 2,150)(1) = | $30 U |
| Beef (10,900 - 10,750)(2) = | 300 U |
| Secret B (8,720 - 8,600)(1.50) = | 180 U |
| Total | $510 U |
The sum of the mix and yield variances must be equal to the material quantity variance. The status of the material quantity variance is determined in the usual way, i.e., it is unfavorable if the actual quantity used exceeds the standard quantity allowed. The mix variance is unfavorable if AQU > AQA, i.e., the actual quantity exceeds the quantity called for by the standard mix. This is unfavorable because it increases the cost of the product. The material yield variances represent a measure of what the material quantity variances would have been if the actual mix proportions were equal to the standard mix proportions. Then AQA would be equal to AQU and the quantity variance and yield variance calculations would be identical. The yield variances are unfavorable when AQA>SQA. In the example presented above, the firm used relatively more of the most expensive material, (beef) which increased the unfavorable quantity variance by $190 more than it would have been if materials had been used in the standard mix proportions, but 21,800 pounds of material had still been used.
Alternative Analysis for Fixed Overhead
Some firms split the production volume variance into two parts. These include the idle capacity variance and the difference between the production volume variance and the idle capacity variance. This is usually called the fixed overhead efficiency variance although the term is misleading.
Idle Capacity Variance = (SFOR)(DH) - (SFOR)(AHU)
= (50)(4,800) - (50)(4,100) = 240,000 - 205,000 = $35,000 unfavorable
The idle capacity variance is 5,000 less unfavorable than the production volume variance ($40,000 from above). Using actual labor hours as the measure of capacity utilization caused this difference.
Fixed Overhead Efficiency Variance = (SFOR)(AHU) - (SFOR)(SHA) = (50)(4,100) - (50)(4,000) = 205,000 - 200,000 = $5,000 unfavorable
The combination of these two variances (35,000 + 5,000) is equal to the production volume variance of $40,000. Some companies interpret the fixed overhead efficiency variance as a measure of the inefficient use, or misuse, of capacity. This interpretation has some appeal when direct labor time represents the main constraint on productive capacity. However, the $5,000 variance represents nothing more than the difference between applied fixed overhead in normal historical costing and applied fixed overhead standard costing. In addition, the term "fixed overhead efficiency variance" is misleading because it appears to imply that direct labor efficiency can influence actual fixed overhead costs. Of course, actual costs are not involved in the calculation.
Twelve Alternative Methods of Overhead Variance Analysis
A wide variety of methods and terminology are found in practice. The following illustrations provide some of the possibilities for the Expando Company example.
| Two Way Analysis Alternatives | ||
| Controllable Variance Uncontrollable Variance (PVV) Total Overhead Variance |
$364,000 - 360,000
= $360,000 - 320,000 = $364,000 - 320,000 = |
$4,000 U 40,000 U $44,000 U |
| Total Variable Overhead Variance Total Fixed Overhead Variance Total Overhead Variance |
$121,500 - 120,000 = $242,500 - 200,000 = |
$1,500 U 42,500 U $44,000 U |
| Three Way Analysis Alternatives | ||
| Controllable Variance Planned Production Volume Variance Unplanned Production Volume Variance Total Overhead Variance |
$364,000 - 360,000
= $240,000 - 221,000 = $221,000 - 200,000 = |
$4,000 U 19,000 U 21,000 U 44,000 U |
| Total V.O. Variance F.O. Spending Variance Production Volume Variance Total Overhead Variance |
$121,500 - 120,000 = $242,500 - 240,000 = $360,000 - 320,000 = |
$1,500 U 2,500 U 40,000 U $44000 U |
| Total Spending Variance V.O. Efficiency Variance Production Volume Variance Total Overhead Variance |
$364,000 - 363,000 = $363,000 - 360,000 = See above |
$1,000 U 3,000 U 40,000 U $44000U |
| Controllable Variance F.O. Efficiency Variance Idle Capacity Variance Total Overhead Variance |
$364,000 - 360,000 = (4,100 - 4,000(50) = (4,800 - 4,100)(50) = |
$4,000 U 5,000 U 35,000 U $44,000 U |
| Total Spending Variance Total Efficiency Variance Idle Capacity Variance Total Overhead Variance |
See above (4,100 - 4,000)(80) = See above |
$1,000 U 8,000 U 35,000 U $44,000 U |
| Four Way Analysis Alternatives | ||
| V.O. Spending Variance F.O. Spending Variance V.O. Efficiency Variance Production Volume Variance Total Overhead Variance |
$121,500 - 123,000 = $242,500 - 240,000 = See above See above |
$1,500 F 2,500 U 3,000 U 40,000 U $44,000 U |
| V.O. Spending Variance F.O. Spending Variance Total Efficiency Variance Idle Capacity Variance Total Overhead Variance |
See above See above See above See above |
$1,500 F 2,500 U 8,000 U 35,000 U $44,000 U |
| Total Spending Variance V.O. Efficiency Variance F.O. Efficiency Variance Idle Capacity Variance Total Overhead Variance |
See above See above See above See above |
$1,000 U 3,000 U 5,000 U 35,000 U $44,000 U |
| Five Way Analysis | ||
| V.O. Spending Variance F.O. Spending Variance V.O. Efficiency Variance Planned Production Volume Variance Unplanned Production Volume Variance Total Overhead Variance |
$121,500 - 123,000 = $242,500 - 240,000 = See above See above See above |
$1,500 F 2,500 U 3,000 U 19,000 U 21,000 U $44,000 U |
| V.O. Spending Variance F.O. Spending Variance V.O. Efficiency Variance F.O. Efficiency Variance Idle Capacity Variance Total Overhead Variance |
See above See above See above See above See above |
$1,500 F 2,500 U 3,000 U 5,000 U 35,000 U $44,000 U |