Chapter 3
Part II: Statistical Process Control
James R. Martin, Ph.D., CMA
Professor Emeritus, University of South Florida
MAAW's Textbook Table of Contents
PART II
STATISTICAL CONTROL CONCEPTS AND TECHNIQUES
STATISTICAL PROCESS CONTROL (SPC) CONCEPT
According to W. Edwards Deming, the main problem in management and leadership is the failure to understand the concept of variation9. This is because effective management requires an understanding of the concept of control which requires the realization that there will always be variation in any cost or process measurement. Control involves an evaluation to determine if the object to be controlled, such as a cost, or process measurement, is inside or outside an acceptable range, i.e., whether it is considered to be "in control", or "out of control". A cost, or process measurement (e.g., a quantity of input or output) that is outside an acceptable range, is viewed as potentially out of control.
Statistical process control or SPC is a method developed by Walter Shewhart10 that has been used extensively by Deming and others in the area of quality control11and extended to the area of cost control by accounting researchers12. The method is applied by establishing a range based on upper and lower limits, rather than establishing a single point estimate as a measure of acceptable performance. These limits are based on the observed variability within a stable, i.e., "in control" system.
The Control Chart
Initially, process measurements are plotted on a chart or graph to determine if the system is stable before control limits are calculated. If the system is stable or predictable, control limits are established in the manner explained below. Once the control limits have been determined, then observations that fall within the limits are attributed to common, or random causes, (i.e., problems of the system), while observations that are outside the control limits are attributed to special causes that may need to be investigated and corrected if they continue to de-stabilize the system.
Stabilizing Versus Improving The System
It is important to understand that eliminating a special cause of a variation is not an improvement in the system. An improvement in a stable system requires a reduction in the variability within the system or an improvement in the mean outcome. Both require changing the system, i.e., the variability that results from common causes.
Plotting Sample Means Rather Than Individual Observations
Although the term observation is used in the discussion above, the data plotted on a control chart normally represents the means of samples of observations, rather than the individual observations. This reduces the risk of making a wrong decision about whether the process is in, or out of control. Evaluating sample means, rather than single observations, also makes it easier to design the control system because the distribution of thirty of more sample means will be normally distributed regardless of the shape of the population sampled. 13
The most common types of control charts include X-bar charts and R charts. The X-bar charts are based on an estimate of the mean of the population parameter being measured, while the R charts are based on an estimate of the range of the population parameter being measured. Both charts are used together for reasons explained below. The X-bar chart is discussed first.
Two estimates are needed to develop an X-bar control chart. These include: 1) an estimate of the mean of the population parameter being measured and 2) an estimate of the variability of the sample means within the population. These estimates are based on the concept of the normal distribution.
Estimate of the Population Mean
If a large number of samples of the parameter being measured are taken (e.g., thirty or more) when the process is stable, or "in control", and the mean is calculated for each sample, these means will represent a sampling distribution that will be approximately normal regardless of the shape of the population sampled. The mean of the sample means is referred to as the grand mean, and is used as an estimate of the mean of the population. The grand mean is calculated as follows:
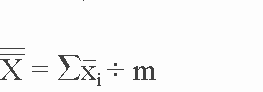
where:
=
X = the grand mean or the mean of the sample means.
_
Xi = the ith sample mean.
m = the number of samples taken, therefore i ranges from 1 to m.
This equation tells us to sum the sample means and then divide by m to obtain the grand mean.
Estimate of the Variability of the Sample Means
As indicated above, the control procedure is normally based on periodically testing whether sample means are within control limits, not whether individual observations are within control limits. To test sample means, we need an estimate of the variability of the population sample means, i.e., all possible means from all possible samples of size n. The actual variability of these means is measured by the standard deviation of the sample means of all possible samples of size n which depends on the standard deviation of the population as follows14:
![]()
where:
S = standard deviation of all possible sample
means of size n,
SD = standard deviation of the population parameter being measured and
n = the number of observations in a sample.
Since the standard deviation of the population parameter is nearly always an unknown, the mean of the sample standard deviations is used as a substitute to obtain an estimate of the standard deviation of all possible sample means as follows:
![]()
where:
^
S = estimate of the standard deviation of sample means from all possible samples of size n and
_
S = mean of the sample standard deviations
from the samples taken15.
Determining the Control Limits for X
After the two estimates are calculated, the control limits are:
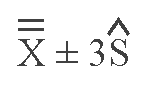
if the sample size is sufficiently large, or
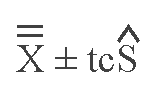
if the sample size is small, where .005 or .001 may be used for c, where
c = (1-confidence level) ÷ 2.
The limits from the grand mean ±3S cover 99.73% of the area under a normal curve, or 99.73% of the random variations in a stable (in control) system when working with a control chart.
Shortcut For Determining 3S Control Limits
Calculating the standard deviation for each sample is time consuming and involves the risk of including arithmetical errors in the analysis. A more convenient procedure for determining 3S control limits uses the mean of the sample ranges. For each sample, the difference between the highest and lowest observations are averaged to find the mean of the sample ranges. Then the 3S control limits are calculated as follows:
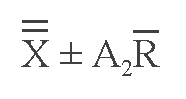
where:
_
R = the mean of the sample ranges and
A2 = a factor from Exhibit 3-9.
The values for A2 were developed by statisticians to facilitate using the shortcut approach.
|
EXHIBIT 3-9 Factors For Control Charts* |
|||
| Sample Size (n) | A2 | D3 | D4 |
|
2 3 4 5 6 7 8 9 10 |
1.880 1.023 .729 .577 .483 .419 .373 .337 .308 |
0 0 0 0 0 .076 .136 .184 .223 |
3.267 2.575 2.282 2.115 2.004 1.924 1.864 1.816 1.777 |
| * These factors can be traced back to Shewhart's original work. | |||
The purpose of developing an X-bar control chart is to provide a way for the analyst to decide when a cost or process mean is in control or out of control. However, the analyst can make two types of errors:
A Type I error is when a random (common) variation is attributed to a special cause, e.g., hold a worker responsible for a problem caused by the system.
A Type II error is when a variation resulting from a special cause is attributed to a common cause, i.e., treated as a random variation.
The analyst can always avoid one type of error or the other, but not both simultaneously, i.e., by continuously avoiding one type of error, the analyst would make the other type of error as often as possible.16 Using ±3 standard deviations in determining the control limits is an attempt to minimize the combined costs of the two types of errors. In general, control limits based on ±3S are used when the cost of investigation is high relative to the possible losses that will result if the process is out of control. If the cost of investigation is low relative to the possible losses from an out of control situation, then the limits could be set at ±2S rather ±3S. This would increase the number of type I errors, but reduce the number of type II errors.
The X-bar chart is well suited to indicate changes in the mean, but a system can be out of control if either the mean changes, or if the standard deviation of the population parameter changes. Since changes in the standard deviation will be reflected by the range measurement, the R chart provides a faster way to spot this type of problem. Although an out of control situation may appear on both charts, one chart will tend to reveal the problem before the other chart. For this reason, both charts are frequently used together.
Control limits for the range are determined as follows:
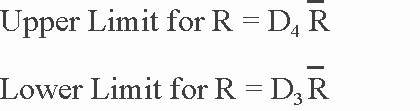
where D4
and D3 are factors from Exhibit 3-9.
Example 3-317
Assume that ten samples of eight observations each were taken of the time (in seconds) required to perform an automated drilling operation. The sample observations, along with mean times and ranges are presented in Exhibit 3-10.
|
EXHIBIT 3-10 Times For Drilling Operation |
|||
| Sample Number | Observations | _ X |
R |
|
1 2 3 4 5 6 7 8 9 10 |
6, 5, 5, 4, 5, 4, 6, 5 6, 6, 7, 5, 7, 5, 4, 5 5, 5, 4, 7, 6, 5, 3, 5 6, 6, 5, 4, 7, 7, 7, 5 4, 6, 6, 7, 8, 4, 5, 5 5, 4, 8, 5, 3, 5, 4, 5 3, 5, 5, 5, 6, 7, 5, 6 6, 6, 6, 5, 5, 4, 5, 5 8, 7, 5, 5, 6, 7, 3, 6 5, 5, 5, 6, 7, 5, 5, 5 |
5.000 5.625 5.000 5.875 5.625 4.875 5.250 5.250 5.875 5.375 53.75 |
2 3 4 3 4 5 4 2 5 2 34 |
From the data in Exhibit 3-10:
=
X = 53.75 ÷ 10 = 5.375
_
R = 34 ÷ 10 = 3.4
Control limits for the X-bar Chart
Control limits for the X-bar chart are calculated as follows:
=
_
X + A2R = 5.375 + (.373)(3.4) = 6.6432 = upper control limit.
=
_
X - A2R = 5.375 - (.373)(3.4) = 4.1068 = lower control limit.
The X-bar chart for the initial data is presented in Figure 3-9.
Control limits for the R-chart
Control limits for the R-chart are determined in the following manner.
_
D4R = (1.864)(3.4) = 6.3376 = upper control limit.
_
D3R = (.136)(3.4) = .4624 = lower control limit.
The range chart for the initial data is presented in Figure 3-10. Both charts show a stable pattern.
Using the Control Chart
Now assume that ten additional samples were taken on a daily basis to monitor the drilling process. The data from these samples is presented in Exhibit 3-11.
|
EXHIBIT 3-11 Times For Drilling Operation |
|||
| Sample Number | Observations | _ X |
R |
|
11 12 13 14 15 16 17 18 19 20 |
5, 6, 6, 5, 7, 6, 5, 5 5, 6, 5, 5, 7 ,6, 5, 3 4, 5, 4, 6, 5, 6, 6, 5 5, 4, 4, 7, 6, 5, 4, 5 5, 5, 4, 6, 6, 6, 4, 5 7, 7, 7, 6, 7, 2, 8, 5 8, 7, 6, 6, 7, 7, 7, 6 6, 5, 4, 5, 5, 7, 4, 5 7, 5, 6, 7, 5, 8, 7, 6 6, 6, 7, 8, 6, 8, 7, 7 |
5.625 5.250 5.125 5.000 5.125 6.125 6.750 5.125 6.375 6.875 |
2 4 2 3 2 6 2 3 3 2 |
The mean drilling times and ranges for the ten new samples are plotted on the charts in Figures 3-11 and 3-12. Observe that the X-bar chart in Figure 3-11 indicates that the process may be out of control for samples 17 and 20. Note also that the range chart seems to indicate that the variability of the process is stable, although the range for sample 16 is very close to the upper control limit. It appears that the mean drilling time has increased, thus an investigation appears to be needed to determine if a special (assignable) cause can be found. Some possible causes for the increase in drilling times include differences in the incoming materials or drill bits. Another possibility is that the drilling equipment needs to be adjusted in some way.
Measuring Improvements in a System
Is there any way for us to determine if the process in the above example is efficient? The answer is no, we cannot evaluate whether the system is good or bad with the available information. An efficient drilling process might be represented by a mean drilling time of 2 seconds with a range of .5 seconds, i.e., 1.75 to 2.25. All we can say is that the process appeared to be stable, or in control, until sample 17 was taken. However, control charts are useful for measuring the effects of changes in the system to see if an improvement has been obtained after a change in the system has been made. There are two types of improvements in a system. One type is an improvement in the mean outcome. The other type is a reduction in the amount of variation, i.e., the range of variation. For example, if the Company changed the process to require higher quality drill bits, the mean drilling times might decrease and the range might also decrease. This would represent an improvement in the process that would be reflected on the old control charts. Then, with additional sample data, new control charts would be developed to monitor the new improved process. Used in this way, statistical process control provides a tool to support continuous improvement, as well as a way to control performance.
THE SPC CONCEPT AND THE DICHOTOMY OF CAPITALISM
As we proceed through this textbook we will examine several accounting methods that are used by management to evaluate and control performance. The standard cost system illustrated in Chapter 10 provides a good example of this type of control methodology. These systems are referred to by critics as top down systems because managers command and control workers in a top down authoritarian fashion. Companies that embrace the individualistic model of capitalism discussed in chapter 1, (most American companies until recently) tend to use this type of top down method. However, companies operating in a communitarian, collectivist, or team oriented system tend to use more bottom up approaches that empower workers to control their own performance. The SPC methodology discussed above provides a good example of a bottom up approach because control charts are used at the operator level to monitor processes on a timely basis, e.g., hour by hour or day by day. These ideas provide some of the background knowledge you will need in practice to deal with the controversial issue of whether top down or bottom up approaches are more effective. We will examine this issue and several related issues as we proceed through this textbook.
9 See Deming, W. E. 1986. Out of the Crisis. Massachusetts Institute of Technology Center for Advanced Engineering Study: 309 and Deming, W. E. 1993. The New Economics for Industry For Industry, Government & Education. Cambridge: Massachusetts Institute of Technology Center for Advanced Engineering Study. (Summary).
10 Shewhart, W. A. 1939. Statistical Method from the Viewpoint of Quality Control. Graduate School, Department of Agriculture, Washington.
11 See Deming, Out of the Crisis.
12 For a review of some of these papers, see Kaplan. R. S. 1975. The significance and investigation of variances: Survey and extensions. Journal of Accounting Research (Autumn): 311-337. See also Onsi, M. 1967. Quantitative models for accounting control. The Accounting Review (April): 321-330. (Comparison of three control models: 1. The traditional standard cost model, 2. a model based on classical statistics, and 3. a model based on decision theory).
13 This phenomenon is referred to as the Central Limit Theorem.
14 The variability of the sample means (S), will be considerably less than the variability of the population parameter (SD), because extreme high and low values will average out.
15 The standard deviation (S) is the square root of the variance. The variance is
calculated as follows:
_
S2 = ∑
(Xi
- X)2 ÷ (n-1)
16 See Deming, Out Of The Crisis: 319.
17 Adapted from Gaynor, E. W. 1954. Use of control charts in cost control. NACA Bulletin (June): 1300-1309.
Questions Related to Part I
1. What is a cost driver?
2. In the equation Y = a + bX, which letters represent
variables and which ones represent constants?
3. Which letter in the equation above represents the slope of
the function? What is the slope?
4. When used as a cost function, which letter in the equation
above represents the cost driver?
5. Do you think most types of cost have a single driver or
multiple drivers? Explain.
6. What are some of the drivers of gasoline costs for an
automobile?
7. Would you expect cost functions to be linear or non-linear?
What do you think would cause a cost function to be non-linear?
8. Why is the high-low method said to be an inferior approach?
9. In what way is the scatter graph or free hand approach
superior to the high-low method?
10. In what way is the simple regression approach superior to
the scatter graph method?
11. What do we mean by least squares?
12. How does a statistic differ from a parameter?
13. Will the simple regression approach identify which
variable is dependent and which variable is independent? Explain.
14. Will correlation analysis identify which variable is
dependent and which variable is independent? Explain.
15. What do we mean when we say that r-square (r2)
represents the proportion of explained variation? Include the total variation
and unexplained variation in your answer.
16. In calculating the standard error of the estimate, why do
we square the error terms?
17. What is the relationship between the unexplained variation
and the standard error of the estimate?
18. Why do we want the calculated t value to be large?
19. How would you test the assumption concerning linearity?
20. Heteroscedasticity indicates that the analyst is not
working with a stable system? Explain.
21. Autocorrelation also represents some type of non-stability
in the data. How do heteroscedasticity and autocorrelation differ?
22. What causes multicollinearity?
23. How do you know when you have a problem with
multicollinearity?
24. Does a negative b value mean you have a problem with
multicollinearity? Explain.
25. Does a negative intercept (a value) mean you have a
problem with multicollinearity? Explain.
26. Do we want the b values to be large or small? Explain.
27. Do we want the standard errors (Se and Sb) to be large or
small? Explain.
28. Do we want the calculated t value to be large or small?
Explain.
(See the SPC Questions for a longer list of questions with links to related materials).
29. In developing a control chart, the analyst recognizes that there are two types of variation in a system. One type of variation is produced by common causes and the other type is generated by special causes. Explain the difference.
30. Why is it important for management to know whether a
variation in performance came from common causes or special causes?
31. Why are control charts developed using sample means?
32. Why do we need both X-bar and R control charts?
33. Does an observation (i.e., sample mean) plotted outside the control limits
necessarily indicate a special cause? Explain.
34. How do confidence intervals differ from the upper and
lower limits of a control chart?
35. Discuss the two types or errors connected with the use of
control charts. What type do you think managers tend to make more often? Why.
36. To say that a system is stable means that the performance
of the system is predictable within a specified range. Explain this statement.
37. Does a stable system mean that the system is efficient?
Explain.
38. How can control charts be used to promote continuous
improvement of a system?
39. Think of some practical applications of the control chart
you could use to monitor your health, the performance of your car, or the
performance of some other system you come in contact with in your daily life.
40. Is the control chart methodology a top down or a bottom up approach? Explain.
PROBLEM 3-9
1. Using the terminology of statistical control charts, a stable system means that the variation within the system is
a. random.
b.
controllable.
c. in control.
d.
a and c.
e. b and c.
2. Normally the area within 3S control limits on an X-bar control chart
a. measures the variation in the mean resulting from common causes.
b. measures the variation in the mean resulting from special causes.
c. represents approximately 95% of the area under a normal curve.
d. a and c.
e. b and c.
3. Which of the following individuals developed the concept of statistical control?
a. Walter A. Shewhart.
b. W. Edwards Deming.
c. Robert S. Kaplan.
d. Edwin W. Gaynor.
e. None of these.
4. When using a statistical control chart, a point outside the control limits is attributed to
a. common or random causes.
b. assignable or special causes.
c. a problem caused by the system.
d. a and c.
e. b and c.
5. Statistical control charts are frequently developed for sample means, rather than individual observations to avoid the problem of
a. non normality.
b. autocorrelation
c. non linearity.
d. range variations.
e. heteroscedasticity.
6. Using the control chart methodology, when a system is said to be stable, this means
a. that the system is efficient.
b. that the variation within the system is controllable.
c. that the variation within the system is predictable.
d. that the performance of the system is improving.
e. none of these.
7. The control limits on a control chart based on the grand mean ±3S include
a. all of the variation resulting from common causes.
b. all of the variation resulting from special causes.
c. over 99% of the variation resulting from common causes.
d. over 99% of the variation resulting from special causes.
e. none of these.
8. The center line on an X-bar control chart is
a. the mean of the sample means.
b. the mean of the predicted values.
c. the mean of the sample standard deviations.
d. the standard deviation of the sample means.
e. the standard deviation of the sample observations.
9. An example of a type I error is where a worker is blamed for a problem caused by the system. An example of a type II error is where the system is blamed for a problem that is not caused by the system. If the control limits were changed from ±3S to ±2S, which of the following would tend to occur?
a. Type I errors would increase while type II errors would decrease.
b. Type II errors would increase while type I errors would decrease.
c. Both types of errors would increase.
d. Both types of errors would decrease.
e. More information is needed to answer this question.
10. In which type of company would the statistical process control methodology tend to be used by individual workers?
a. A company that embraces the individualistic model of capitalism.
b. A company that embraces the communitarian model of capitalism.
c. Both a or b equally.
d. Neither a or b.