Chapter 14: Appendix 14-2
Input-Output Accounting
Illustration with Profit Centers and Transfer Pricing
James R. Martin, Ph.D., CMA
Professor Emeritus, University of South Florida
Chapter 14 | MAAW's Textbook Table of Contents
Input-output accounting extends Leontief's input-output economic analysis to a variety of problems in accounting. In this brief introduction to the topic the input-output accounting technique involves using matrix algebra to solve a variety of cost allocation and transfer pricing problems that include complicating factors such as reciprocal intersegment transfers, fixed cost allocations and self-service. The segments may be cost centers (including service departments as in Chapter 6), profit centers, or investment centers (See the Responsibility Accounting topic and Chapter 14). The technique is explained and illustrated below using the following simple example.
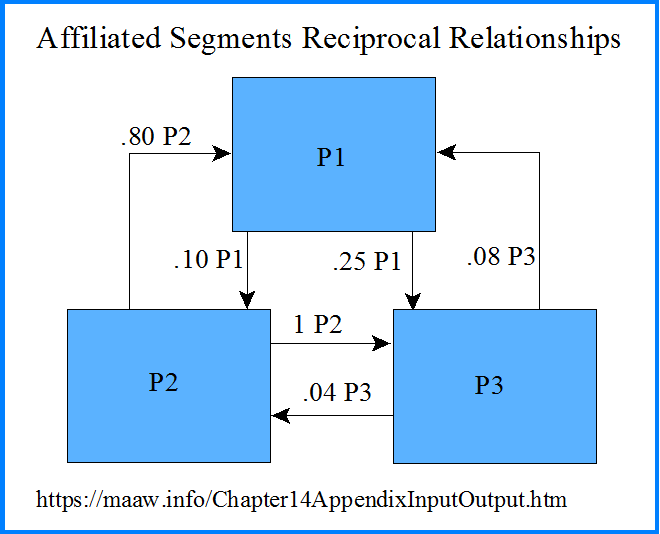
Assume three affiliated segments each produce a single product. Segment 1 produces product 1, Segment 2 produces product 2, and Segment 3 produces product 3. The standard quantities of variable inputs per output are presented below.
| Segment | Type of Input | Standard Quantity | Standard Price | Standard Cost Per Unit |
| 1 |
D.M D.L. V. Ovhd Product 2 Product 3 |
4.00 units .08 hrs .08 hrs .80 units .08 units |
$.10 5.00 10.00 ? ? |
$.40 .40 .80 ? ? |
| 2 |
D.M. D.L. V. Ovhd Product 1 Product 3 |
.50 units .05 hrs .05 hrs .10 units .04 units |
$.90 3.00 12.00 ? ? |
$.45 .15 .60 ? ? |
| 3 |
D.M. D.L. V. Ovhd Product 1 Product 2 |
.50 units .19 hrs .19 hrs .25 units 1.00 units |
$2.60 5.00 25.00 ? ? |
$130. .95 4.75 ? ? |
The reciprocal relationships between the three segments are illustrated in the graphic below.

Outside or unaffiliated sales for the three products are budgeted at 25 units of product 1, 70 units of product 2, and 30 units of product 3. Market prices are budgeted at $6.00 for product 1, $3.00 for product 2, and $15 for product 3. Assume that there are no fixed costs, selling and administrative expenses, or self-service, i.e., self-consumption.
Required:
1. Calculate the standard variable cost per unit for each segment's output.
2. Calculate the required total quantities of each segment's output based on the budgeted outside or unaffiliated sales level given?
3. Calculate the transfers required between segments.
4. Prepare segmented and consolidated statements based on transfers at: a. standard variable cost, and b. market prices.
THE INPUT-OUTPUT TECHNIQUE
To solve this problem the user must identify the input-output relationships as indicated in the first set of equations below, and then rearrange them (to preserve vertical symmetry) as indicated in the second set of equations. In these equations C represents the standard variable cost per output for each segment, e.g., C1 is the standard variable cost per hour of service provided by segment 1.
C1 = .80C2 + .08C3 + 1.60
C2 = .10C1 + .04C3 + 1.20
C3 = .25C1 + 1.00C2 + 7.00
1.00C1 - .80C2 - .08C3 = 1.60
-.10C1 + 1.00C2 - .04C3 = 1.20
-.25C1 - 1.00C2 + 1.00C3 = 7.00
When the second set of equations is expressed in the matrix form AC = B, then A represents the matrix of coefficients on the left-hand side, i.e., the input-output coefficients, C represents the matrix of unknown standard variable cost per output for each segment, and B represents the matrix of right-hand side values, i.e., the variable input costs per output that are known before the equations are solved simultaneously. These values represent the segments' direct variable costs.
The solution is generated in the following manner. The standard variable unit costs are found by calculating the inverse of A and multiplying by B, i.e.,
C = A-1 B
where C is the matrix of standard variable costs per output, A-1 is the inverse of the matrix A, and B is the matrix of direct variable cost for each segment. Before fixed costs can be included in the calculations, the total required segment outputs must be calculated. This is accomplished in the following manner:
X = T-1 Y
where X represents the matrix of total outputs required to satisfy the outside or unaffiliated demands, T-1 represents the transpose of A-1 (i.e., the rows of A-1 become the columns of T-1 , and Y represents the matrix of outside demands. Note that X might be considerably larger than Y because of the intersegment requirements.
After the total required outputs have been calculated, the standard total costs per output may be found by adding the unit fixed cost for each segment (i.e., segment fixed costs divided by segment total output) to the right-hand side values, and then resolving for C as follows:
C = A-1 (B+F)
where C becomes the matrix of standard total costs per output, and F represents the matrix of unit fixed costs based on planned sales and production, i.e., X.
The required transfers and self-services (or self-consumption) are calculated in the manner indicated below:
U = I - T
Ri,j = Ui,jXi
where T is the transpose of A, I is an identity matrix ( i.e., it has ones down the main diagonal I(1,1), I(2,2), etc. and zeros everywhere else), and Ri,j represents the quantity transferred from segment i to segment j. For example, the following calculation shows how the transfer from segment 1 to segment 2 would be calculated.
R1,2 = U1,2X1
Solution to the Illustration
| Product or Service |
Standard
Variable Cost Per Unit |
Total
Outputs Required |
Outside or Unaffiliated Demand |
Cost of
Outside Sales at Standard Cost |
| 1 | 4.000 | 50 | 25 | 100 |
| 2 | 2.000 | 150 | 70 | 140 |
| 3 | 10.000 | 40 | 30 | 300 |
| From Segment | To Segment | Self-Service and Transfers in Units* |
Self-Service
and Transfers at Standard Variable Cost |
| 1 1 1 2 2 2 3 3 3 |
1 2 3 1 2 3 1 2 3 |
0 15 10 40 0 40 4 6 0 |
0 60 40 80 0 80 40 60 0 |
| * The applicable unit of measure of the sending segment. | |||
| Transfers Based on Standard Variable Cost | ||||
| Segment | Sales $ Unaffialated |
Transfers at
Standard Variable Cost |
Variable Operating Cost* |
Operating Income |
| 1 | 150 | 100 | 200 | 50 |
| 2 | 210 | 160 | 300 | 70 |
| 3 | 450 | 100 | 400 | 150 |
| Eliminations | 360 | 360 | ||
| Consolidated | 810 | 540 | 270 | |
| * Operating Cost = Cost transferred into the segment plus the direct variable cost. | ||||
| Transfers Based on Market Prices | ||||
| Segment | Sales
$ Unaffialated |
Transfers
at Market Prices |
Variable Operating Cost* |
Operating Income |
| 1 | 150 | 150 | 260 | 40 |
| 2 | 210 | 240 | 360 | 90 |
| 3 | 450 | 150 | 460 | 140 |
| Eliminations | 540 | 540 | ||
| Consolidated | 810 | 540 | 270 | |
| * Operating Cost = Cost transferred into the segment plus the direct variable cost. | ||||
______________________________________
For more on Input-Output Accounting see the following:
Feltham, G. A. 1970. Some quantitative approaches to planning for multiproduct production systems. The Accounting Review (January): 11-26.
Gambling, T. E. 1968. A technological model for use in input-output analysis and cost accounting. Management Accounting(December): 33-38.
Gambling, T. 1971. Input-output analysis and the cost model: A reply. The Accounting Review (April): 376-379.
Ijiri, Y. 1968. An application of input-output analysis to some problems in cost accounting. Management Accounting (April):49-61.
Livingstone, J. L. 1968. Matrix algebra and cost allocation. The Accounting Review (July): 503-508.
Livingstone, J. L. 1969. Input-output analysis for cost accounting, planning and control. The Accounting Review (January): 48-64.
Livingstone, J. L. 1970. Management Planning and Control: Mathematical Models. McGraw-Hill.
Livingstone, J. L. 1973. Input-output analysis for cost accounting, planning and control: A reply. The Accounting Review (April): 381-382.
Manes, R. P. 1965. Comment on matrix theory and cost allocation. The Accounting Review (July): 640-643.
Shank, J. K. 1972. Matrix Methods in Accounting. Addison-Wesley.
Staubus, G. J. 1971. Activity Costing And Input-Output Accounting. Irwin. See Chapter 8.
Input-Output Accounting Main Page