Chapter 14
Investment Centers, Return on Investment, Residual Income and Transfer Pricing
James R. Martin, Ph.D., CMA
Professor Emeritus, University of South Florida
MAAW's Textbook Table of Contents
The purpose of this chapter is to: 1) discuss two common performance measurements for investment centers and the various relationships between these measurements, 2) present some equations related to these measurements that can be used for planning purposes, 3) discuss a number of issues related to how these measurements are calculated and 4) discuss the transfer pricing problem that arises when investment centers sell products or services to each other.
The two measurements commonly used to evaluate investment centers are Return on Investment (ROI) and Residual Income (RI). This chapter includes three main sections. The ROI measurement is discussed in the first section, followed by a discussion of RI and finally the issues related to transfer pricing are discussed in the last section. An Appendix is also included related to the conflict between choosing investment projects and evaluating the subsequent results.
Two Ways to Calculate Return On Investment:
Return on investment or ROI = Net Income ÷ Investment
An alternative formulation of ROI based on Du Pont's formula is as follows:
ROI = (Capital Turnover Ratio)(Profit Margin on Sales)
= (Sales ÷ Investment)(Net Income ÷ Sales)
The Capital Turnover Ratio (CTR) reflects management's ability to generate sales from a given investment base. Note that the source of the investment (i.e., debt or stockholders equity) is usually considered irrelevant, but see alternatives below.
The Profit Margin is the Rate of Return on Sales (ROS) and measures management's ability to control the spread between prices and costs. Productivity and cost control are reflected in this measure as well as other factors such as the sales level.
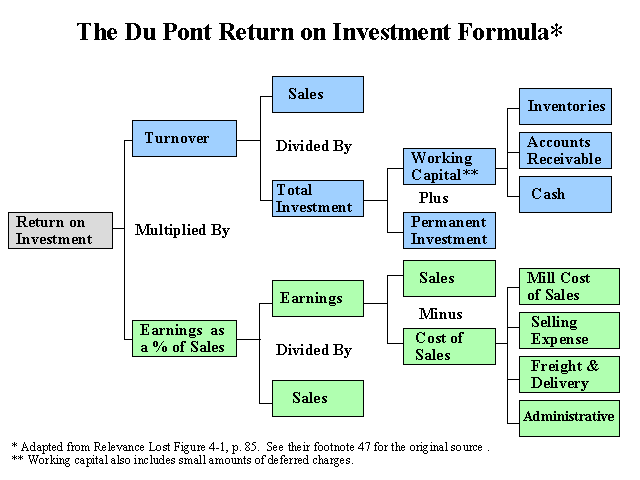
A more detailed view of the Du Pont ROI formula appears in the graphic illustration below1.
ROI may be increased in various ways. Some possibilities include the following.
1. Increasing Capital Turnover (CTR)
a. Increase sales with the same the investment base.
b. Decrease the investment base with the same sales level.
2. Increasing Profit Margin or Return on Sales (ROS)
a. Increase prices with no unfavorable effects on sales.
b. Decrease cost with no unfavorable effects on quality or increase in assets.
c. Increase sales with no changes in prices or costs.
The following diagram (referred to as a Read diagram2) illustrates various combinations of turnover (CTR) and margin (ROS) required to provide three illustrative rates of return (ROI). For example, a 20% ROI can be obtained with a turnover of 2.5 and a margin of 8%, a turnover of 2 and a margin of 10%, or a turnover of 1 and a margin of 20%. A lower turnover requires a higher margin to produce the same ROI.
Relationships Between Sales, Capital Turnover Ratio and Return on Sales Ratio(ROS)
The purpose of this section is to connect Cost-Volume-Profit analysis (MAAW's Chapter 11) with Return on Investment analysis. More specifically, the purpose is to show the relationships between the Return on Sales Ratio (ROS), Sales, and the Contribution Margin Ratio (CMR). The simplifying assumptions of conventional linear CVP analysis are applicable to the analysis presented below. (See Chapter 11 for these assumptions).
Where P = Sales Price, V = Variable cost per unit, TFC = Total Fixed Costs, X = Units produced and sold, CMR = Contribution margin ratio, S = Sales Dollars, NIBT = Net Income Before Taxes, and NIAT = Net Income After Taxes.
The Contribution Margin Ratio (From Chapter 11) is
CMR = (P-V) ÷ P or 1 - V÷P
The Contribution Margin Ratio after taxes (From Chapter 11) is
CMR after taxes = (1-T)(CMR) = (1-T)[(P-V) ÷ P] or (1-T)(1 - V÷P)
An equation for Return on Sales can be developed in terms of units (X) or Sales Dollars (S) as indicated in the table below.
|
Exhibit 14-1 Equations for Return on Sales (ROS) |
|
| Using Units (X) | Using Sales Dollars (S) |
| The Return on Sales Ratio before taxes is: | |
| ROS = NIBT ÷ PX ROS = [(P-V)X - TFC] ÷ PX When X > 0 ROS = [(P-V) ÷ P] - (TFC ÷ PX) ROS = CMR - [(TFC÷P) ÷ X] For Cal Company: (See Chapter 11). P =10, V = 6, TFC = $120,000. ROS = [(10-6) ÷ 10] - (120,000÷10) ÷ X) ROS = .4 - (12,000 ÷ X) For example, what is the return on sales before taxes when 60,000 units are produced and sold? ROS before taxes = .4 - (12,000 ÷ 60,000) = .4 - .2 = .2 or 20% |
ROS = NIBT ÷ S ROS = [S - (V÷P)(S) - TFC] ÷ S When S > 0 For Cal Company: ROS = (1-.6) - (120,000÷S) For example, what is the return on sales before taxes when sales = $600,000? ROS before taxes = .4 - (120,000÷600,000) |
| The Return on Sales Ratio after taxes is: | |
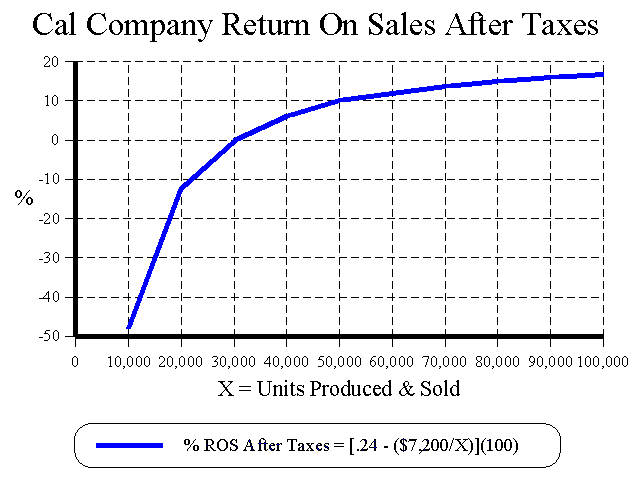
| ROS = NIAT ÷ PX ROS = [(1-T)(P-V)(X) - (1-T)(TFC)] ÷ PX When X > 0 ROS = [(1-T)(P-V) ÷ P] - [(1-T)(TFC) ÷ PX] ROS = (1-T)(CMR) - [(1-T)(TFC÷P) ÷ X] For Cal Company: ROS = [(1-.4)(10-6)÷10] - [(1-.4)(120,000÷10) ÷X] ROS = .24 - (7,200 ÷ X) For example, what is the return on sales after taxes when 60,000 units are produced and sold? ROS after taxes = .24 - (7,200 ÷ 60,000) = .24 - .12 = .12 or 12%. |
ROS = NIAT ÷ S ROS = [(1-T)(S - (V÷P)(S) - TFC)] ÷ S When S > 0 ROS = .24 - (72,000÷S) For example, what is the return on sales after taxes when Sales = $600,000? ROS after taxes = .24 - (72,000 ÷ 600,000)
|
Equations For X and S Needed For a Desired ROS
The equations for ROS can be restated in terms of X and S to find the break-even point in units or sales dollars, and the number of units or sales dollars needed to produce a certain ROS. These equations are presented in the table below.
|
Exhibit 14-2 Equations for ROS Stated in Terms of X and S |
|
| Using Units (X) | Using Sales Dollars (S) |
| ROS
before taxes = CMR - [(TFC÷P) ÷ X] Stated in terms of X: ROS - CMR = - (TFC÷P) ÷ X X(ROS - CMR) = -TFC÷P X = (-TFC÷P) ÷ (ROS-CMR) AT the BEP ROS = 0 X = -12,000 ÷ (0-.4) X = 30,000 units |
ROS before taxes = CMR - (TFC÷S) Stated in terms of S: ROS - CMR = -TFC÷S S(ROS-CMR) = -TFC S = -TFC ÷ (ROS-CMR) AT the BEP ROS = 0 S = -120,000 ÷ (0-.4) S = $300,000 |
| If the desired ROS
before taxes is 20% X = -12,000 ÷ (.2-.4) X = -12,000 ÷ -.2 X = 60,000 units |
If the desired
ROS after taxes is 20% S = -120,000 ÷ (.2-.4) S = -120,000 ÷ -.2 S = $600,000 |
| The after tax equation for X | The after tax equation for S |
| X = (1-T)(-TFC÷P) ÷ (1-T)(ROS-CMR) | S = (1-T)(-TFC) ÷ (1-T)(ROS-CMR) |
Some Questions to Emphasize the ROS Relationships
1. What is the relationship between the contribution margin ratio (CMR) and the return on sales ratio (ROS) ?
The Contribution Margin Ratio sets the limit for the Return on Sales Ratio. The return on sales ratio before taxes would be equal to the contribution margin ratio if there were no fixed costs (See equation) and the ROS after taxes would be equal to the CMR multiplied by 1- the tax rate (See equation).
2. What is the relationship between sales and the return on sales ratio (ROS)?
When fixed costs are present, the return on sales ratio (ROS) depends on the level of sales. The graphic illustration below shows Cal Company's ROS after taxes for various sales levels. The Contribution Margin Ratio after taxes (.24 for Cal Company) sets the limit for the after tax ROS. As unit sales increase, the ROS after taxes increases at a decreasing rate and approaches (but can never quite reach) the after tax CMR. Theoretically, if there were no demand or capacity constraints, the maximum ROS after taxes would be slightly less than the contribution ratio after taxes, i.e., (1-T)(CMR) or .24 in the Cal Company example. This is indicated in the equation ROS = .24 - (7,200 ÷ X). If the desired ROS is greater than the CMR, the values for X and S become negative, i.e., outside the feasible solution space. Use the equations stated in terms of X and S to see that this is true.
3. Assume that Cal Company has $500,000 in total assets. What is the ROI after taxes when 60,000 units are produced and sold?
There are two ways to solve this problem.
Calculate ROI = (ROS)(CTR) or calculate NI ÷ Total Assets.
Using the first approach, the ROS after taxes is .24 - (7,200 ÷ 60,000) = .12 or 12% based on the equation developed and explained above.
The Capital Turnover Ratio (CTR) = PX ÷ Investment = (10)(60,000) ÷ 500,000 = 1.2
The ROI after taxes = (ROS)(CTR) = (.12)(1.2) = .144 or 14.4%
Using the second approach, Net Income after taxes is -72,000 + 2.4X (See Figure 11-18).
NI after taxes = -72,000 + 2.4(60,000) = $72,000.
ROI after taxes = NI after taxes ÷ Total Assets = $72,000 ÷ $500,000 = .144 or 14.4%.
Cal Company's CTR, ROS and ROI measurements for various sales levels are provided in the table below and plotted on the graph below the table.
| Unit Sales | Capital Turnover Ratio | ROS After Taxes | ROI After Taxes |
| 10,000 | 0.2 | -.48 | -.096 |
| 20,000 | 0.4 | -.12 | -.048 |
| 30,000 | 0.6 | 0 | 0 |
| 40,000 | 0.8 | .06 | .048 |
| 50,000 | 1.0 | .096 | .096 |
| 60,000 | 1.2 | .12 | .144 |
| 70,000 | 1.4 | .137 | .1918 |
| 80,000 | 1.6 | .15 | .240 |
| 90,000 | 1.8 | .16 | .288 |
| 100,000 | 2.0 | .168 | .336 |
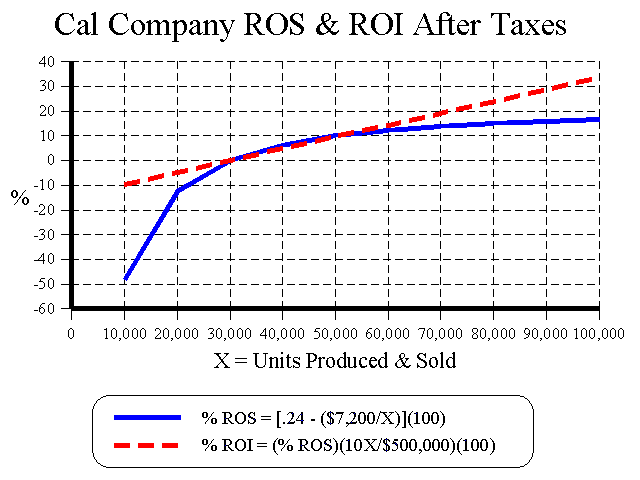
Note that although the function for ROS is non-linear, the function for ROI is linear. This is because Net Income before and after taxes are linear functions in CVP analysis. See Figure 11-18 for a graphic view of Cal Company's CVP analysis. Also note that increasing sales automatically increases the ROS, CTR and ROI even though the CMR remains constant in the conventional linear analysis. The ROS increases at a decreasing rate, while the CTR and ROI increase at a constant rate. The CMR affects the ROI through the effect it has on the ROS.
Equations For X and S Needed For a Desired ROI
The purpose of this section is to show how the ROI equations can be stated in terms of units (X) and sales dollars (S) so that the number of units, or sales dollars needed to produce a desired ROI can be determined. The simplifying assumptions of conventional linear CVP analysis are applicable to the analysis presented below. (See Chapter 11 for these assumptions).
Where P = Sales Price, V = Variable cost per unit, TFC = Total Fixed Costs, NI = Net Income, I = Investment, CMR = Contribution margin ratio, X = Units produced and sold, S = Sales Dollars and T is the tax rate.
|
Exhibit 14-3 Equations For ROI Stated in Terms of X and S |
|
| Using Units (X) | Using Sales Dollars (S) |
| ROI before taxes = NIBT ÷ I
ROI = [(P-V)(X) - TFC] ÷ I X = [(I)(ROI) + TFC] ÷ (P-V) For Cal Company: P =10, V = 6, X = [(500,000)(ROI) + 120,000] ÷ (10-6) How many units need to be produced and sold to generate a ROI of 24% before taxes? X = (125,000)(.24) + 30,000 |
ROI before taxes = NIBT ÷ I
ROI = [(1-V÷P)(S) - TFC] ÷ I S = [(I)(ROI) + TFC] ÷ CMR For Cal Company: P = 10, V = 6, CMR = .4, S = [(500,000)(ROI) + 120,000] ÷ .4 How many sales dollars are needed to generate a ROI of 24% before taxes? S = (1,250,000)(.24) + 300,000 |
| ROI after taxes = NIAT ÷ I
ROI = [(1-T)(P-V)(X)-(1-T)(TFC)] ÷ I X = [(I)(ROI) + (1-T)(TFC)] ÷ (1-T)(P-V) For Cal Company: P =10, V = 6, T = .4 X =[(500,000)(ROI) + (.6)(120,000)] ÷(.6)(.4) How many units need to be produced and sold to generate a ROI of 14.4% after taxes? X = [(500,000)(.144) + 72,000] ÷ 2.4 X = 60,000 units. |
ROI after taxes = NIAT ÷ I
ROI = [(1-T)(1-V÷P)(S) - (1-T)(TFC)] ÷ I S = [(I)(ROI) + (1-T)(TFC)] ÷ (1-T)(CMR) For Cal Company: P =10, V = 6, CMR = .4, S = [(500,000)(ROI) + (.6)(120,000)] ÷(.6)(.4) How many sales dollars are needed to generate a ROI of 14.4% after taxes? S = [(500,000)(.144) + 72,000] ÷ .24 S = $600,000 |
Equations for Multiple Product Companies
All of the equations presented above (for ROS, ROI and X and S for a desired ROS and ROI) can be converted to multi-product situations. We simply need to use weighted averages for contribution margin per unit and the CMR as in the multi-product CVP analysis in Chapter 11, and define X and S in the equations as mixed units and mixed sales dollars. When P and V are involved, these measures also need to be stated in terms of weighted averages.
Sandlot Cap Company Two Products Example
The Sandlot Cap Company produces baseball caps in two categories referred to as regular logo (X1) and special logo (X2). Sales prices, variable costs and sales mix ratios are provided below.
| Product | Price $ | Variable
Cost Per Unit $ |
Mix Ratio Based on Units |
| X1 X2 |
4 8 |
3 5 |
.75 .25 |
The company’s total fixed costs are $300,000, total assets are $1,000,000 and the tax rate is 40%. The mix ratios above indicate that 75% of the units sold are X1s and 25% are X2s. Mix ratios based on sales dollars are .6 for X1 and .4 for X2. These ratios represent each products proportion of the weighted average price. (See Chapter 11 for the CVP analysis related to this company). Based on the simplifying assumptions of conventional linear CVP analysis, determine the following.
1. The number of caps that need to be produced and sold to earn a 30% ROI before taxes?
2. The number of sales dollars needed to earn a 30% ROI before taxes? Solve this in dollars, rather than using your answer to question 1.
3. The number of caps that need to be produced and sold to earn an 18% ROI after taxes?
4. The number of sales dollars needed to earn an 18% ROI after taxes? Solve this in dollars, rather than using your answer to question 3.
5. What are the return on sales and capital turnover ratios when ROI after taxes is 18%?
The solutions to these problems appear below. Note that the equations in Exhibit 14-4 are the same as those in Exhibit 14-3, except X becomes mixed units and S becomes mixed sales dollars.
|
Exhibit 14-4 Sandlot Cap Company Equations For ROI Stated in Terms of X and S for Multiple Products |
|
| Using Mixed Units (X) | Using Mixed Sales Dollars (S) |
|
1. X = [(I)(ROI) + TFC] ÷ (P-V) X = [(1,000,000)(.3) + 300,000] ÷ 1.50 X = 600,000 ÷ 1.50 X = 400,000 mixed units X1 = (.75)(400,000) = 300,000 |
2. S = [(I)(ROI) +
TFC] ÷ CMR S = [(1,000,000)(.3) + 300,000] ÷ .3 S = 600,000 ÷ .3 S = 2,000,000 mixed sales dollars S1 = (.6)(2,000,000) = $1,200,000 |
| 3. X = [(I)(ROI) + (1-T)(TFC)] ÷ (1-T)(P-V) X = [(1,000,000)(.18) + (1-.4)(300,000)] ÷ (1-.4)(1.50) X = (180,000 + 180,000) ÷ .90 X = 400,000 mixed units |
4. S = [(I)(ROI) + (1-T)(TFC)] ÷ (1-T)(CMR) S = [(1,000,000)(.3) + (1-.4)(300,000)] ÷ (1-.4)(.3) S = (180,000 + 180,000) ÷ .18 S = 2,000,000 mixed sales dollars |
5. ROS after taxes = NIAT ÷ Sales
NIAT = -(1-T)(TFC) + (P-V)(X)
NIAT = -(1-.4)(300,000) + (1.5)(X)
NIAT = -180,000 + (.9)(400,000)
NIAT = $180,000
ROS = 180,000 ÷ PX
ROS = 180,000 ÷ (5)(400,000)
ROS = 180,000 ÷ 2,000,000
ROS = .09 or 9%
CTR = Sales ÷ Total Assets
CTR = 2,000,000 ÷ 1,000,000
CTRatio = 2
Checking:
ROI = (ROS)(CTR)
ROI = (.09)(2) = .18
Note and Summary of Equations
Although the conventional linear analysis presented above ignores various non-production related cost drivers revealed in activity-based costing, it emphasizes the fact that increasing sales volume is the most effective way to increase profitability. When sales increases, the ROS, CTR and ROI all increase automatically in the absence of a substantial increase in fixed costs.
| Equations Developed and Used in the Analysis Above | |
| Using Units (X) | Using Sales Dollars (S) |
| ROS = CMR - [(TFC÷P) ÷ X] | ROS = CMR - (TFC÷S) |
| ROS = (1-T)(CMR) - [(1-T)(TFC÷P) ÷ X] | ROS = (1-T)(CMR) - (1-T)(TFC÷S) |
| X = (-TFC÷P) ÷ (ROS-CMR) | S = -TFC ÷ (ROS-CMR) |
| X = (1-T)(-TFC÷P) ÷ (1-T)(ROS-CMR) | S = (1-T)(-TFC) ÷ (1-T)(ROS-CMR) |
| ROI = [(P-V)(X) - TFC] ÷ I | ROI = [(1-V÷P)(S) - TFC] ÷ I |
| X = [(I)(ROI) + TFC] ÷ (P-V) | S = [(I)(ROI) + TFC] ÷ CMR |
| ROI = [(1-T)(P-V)(X)-(1-T)(TFC)] ÷ I | ROI = [(1-T)(1-V÷P)(S) - (1-T)(TFC)] ÷ I |
| X = [(I)(ROI) + (1-T)(TFC)] ÷ (1-T)(P-V) | S = [(I)(ROI) + (1-T)(TFC)] ÷ (1-T)(CMR) |
Possible Investment Bases for ROI
The question concerning how the investment should be measured is controversial. Various possibilities include the following.
1. Total assets available. This is considered to be the best overall measurement if the manager has control over all the assets. However, there is a problem in determining how to value the assets. This problem is discussed below.
2. Total assets employed. These are operating assets currently used. Since this base excludes excess or idle assets such as vacant land or construction in progress it may be appropriate if some of the assets are not under the control of the manager.
3. Net Working Capital plus other assets), i.e., Total Assets Less Current Liabilities. This measurement increases the ROI because it reduces the investment base and allows for the use of short term credit in the manager's performance measurement.
4. Stockholder's Equity or Net Worth. This basis provides a measure of both operating performance and financial leverage. The measurement of financial leverage is the difference between the ROI and the ROSE. Using ROSE creates a bias to increase debt or leverage and risk.
How to Measure Assets for ROI Calculation
The question concerning how assets should be valued is also controversial? Some possibilities include:
1. Gross Book Value, i.e., historical cost. This may encourage managers to dispose of old assets too soon, where assets are still useful, but not very efficient, i.e., disposal value < present value of expected net cash inflows. This measurement favors old divisions with lower cost during inflationary periods.
2. Net Book Value, i.e., historical cost less depreciation. Since the ROI would tend to increase as the asset is depreciated (i.e., because the investment base decreases, the capital turnover ratio would increase), using net book value may encourage managers to keep old assets too long, i.e., beyond the point where the disposal value > present value of the expected net cash inflows. If new assets were purchased, the ROI would decline. This method also favors older divisions.
3. Replacement Cost or Current Cost, i.e., cost of identical assets or similar assets that would provide the same level of service. This may be more equitable for comparing different age divisions, but creates the problem of determining current value for all assets. Total present value (i.e., discounted expected future net cash inflows) or appraisal value can be used to approximate current cost.
RI Alternative to ROI
Residual Income (RI) was developed as an alternative to the return on investment (ROI) measurement to overcome some problems discussed below.
RI = Net Income - Minimum Desired Net Income.
The minimum desired rate of return used in the RI calculation is usually referred to as the cost of capital. The cost of capital is a weighted average measure of the cost of long term debt and stockholders equity.
A relatively new term for this measurement is Economic Value Added (EVA®). This is the Stern Stewart trademarked version of the concept defined as adjusted operating income minus a capital charge. Stern Steward recommend a fairly large number of adjustments although the main concept of Residual Income and EVA® are the same. An underlying assumption is that a manager’s actions only add economic value when the resulting profits exceed the cost of capital.
Maximizing ROI and RI or EVA® are different objectives
Using ROI as a performance measurement may cause many managers to reject profitable projects if the projects would tend to lower the ROI. As a result, a conflict arises between the goals of the manager and the goals of the organization, i.e., goal congruence is not obtained.
Example:
Assume a firm has a minimum desired rate of return of 15 percent after taxes. Recent results show the following for a division:
Assume that Net Income after taxes = $20,000 and Total Assets = $100,000.
ROI = 20%
RI = ($20,000 - 15,000) = $5,000.
Would a manager evaluated on the basis of the ROI accept a new project with an expected return of 16, 18 or 19 percent? Probably not, since it would reduce the division's overall ROI below 20%.
Would the manager accept the project if RI is used as the evaluation measurement. Yes, since the return is above 15%, it would increase the division's residual income.
Separate Problem for RI users
Using Residual Income avoids the problem stated above, but creates a different problem. Using RI makes it difficult to compare the performance of different size divisions.
A partial solution is to compare each division against a negotiated budget for that division. Different size divisions and different aged divisions cannot be adequately compared with either measurement ROI or RI.
Decentralization means the freedom to make decisions. Decentralization can transform a profit center into an investment center. Centralization can transform an investment center into a profit center or transform a profit center into a cost center.
Potential Benefits from Decentralization
1. Better decisions can be made at the local level.
2. Provides more incentives to segment managers.
3. Encourages internal competition.
4. Provides top management with more time for strategic planning and other policy decisions.
Cost of Decentralization
1. Lack of Goal congruence.
2. Conflicts between divisions.
3. Redundant activities.
The greater the interdependence between divisions, the greater the likelihood that the costs of decentralization will be greater than the benefits.
Transfer Prices
A transfer price refers to the price used for intra-company transfers, i.e., transfers between segments of a company. The term transfer pricing normally means pricing transfers between divisions, but could be used in any situation where the output of one segment (e.g., department, operation, process) becomes the input for another segment within the same company.
Three Decisions
A transfer pricing situation usually involves three questions or decisions.
1. Should the transfer take place? This is essentially a "Make or Buy" question. Should the company make the item or outsource, i.e., purchase it on the outside market? This is a relevant cost problem (also referred to a differential or incremental cost). The key is which costs will be different under the two alternatives, i.e., make inside and transfer, or buy from outside the company?
2. If the answer to question one is yes, then what transfer price should be used?
3. Should the central office interfere in establishing the transfer price?
Objectives of Transfer Prices
The overall objective is to establish a transfer price that will motivate effort and goal congruence. There are at least three underlying objectives.
1. To aid in Evaluating Division Performance, i.e., investment centers or profit centers. If the divisions are treated as investment centers, then Return on Investment (ROI) and Residual Income (RI) are the relevant measurements. For profit centers, contribution margin, segment margin, or net income would be a more appropriate measurement.
2. To maintain Division Autonomy. Since autonomy means decentralization and freedom to make decisions, it is also an ingredient in motivating effort. Remember, however, that effort and goal congruence are different. Managers may exert considerable effort in pursuing their own goals that conflict with the goals of the firm. Central office interference in a transfer pricing dispute will affect autonomy and effort. The dilemma is that goal congruent behavior may not be obtained with or without interference.
3. To provide the buying segment with the information necessary for the make or buy question. Intra-company profits included in a transfer price make it impossible for the buying division to answer the make or buy question.
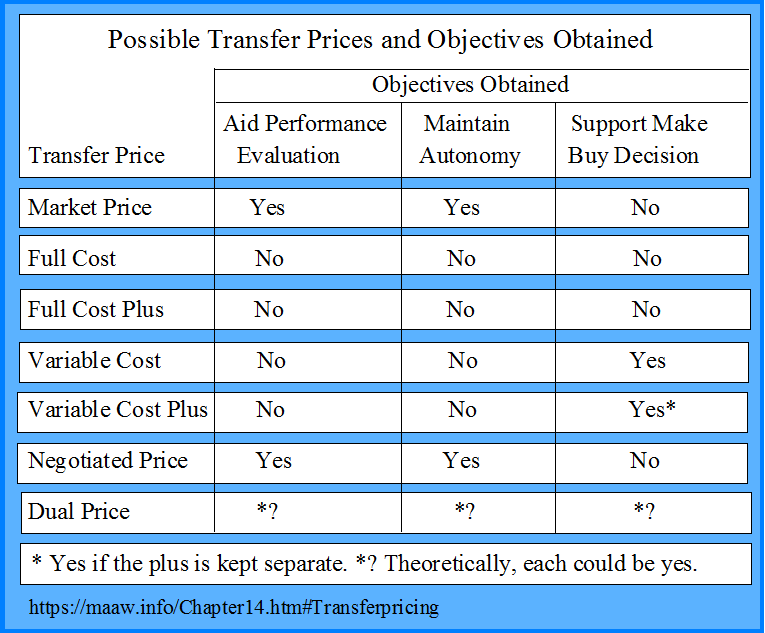
Possible Transfer Prices
1. Market prices. A market price is considered best if the market is perfectly competitive, i.e., if a single buyer or seller cannot affect the price. Generally intra-company transfers at market prices accomplish objectives 1 and 2, but not 3. Unfortunately, several problems occur when trying to use market prices:
a. Most markets are not perfectly competitive. In other words, the demand curve and price structure may shift if the firm buys outside.
b. Market prices may not exist for some products.
c. A market price may not be comparable because of differences in quality, credit terms, or extra services provided.
d. Price quotations may not be reliable because they are based on temporary distress or dumping conditions.
e. A market price may not be relevant because the selling division would not have the same transportation cost, accounting cost for A/R,
credit etc. as an outside supplier.
f. Information for the make or buy decision would not be available to the buying division.
2. Full cost. All manufacturing, selling and administrative cost are included.
The problems that occur when full cost is used as a transfer price include:
a. Transfer prices based on full cost do not accomplish any of the objectives stated above. The selling division could not be evaluated as a
profit center or investment center since it is treated as a cost center.
b. The seller would be motivated to over allocate cost to the product transferred.
c. If actual cost are transferred, the cost of inefficiency will be passed along to the buying division. Thus, standard cost make better
transfer prices although standards may be rigged.
d. The buyer would not have the differential cost information needed for the overall firm make or buy decision. The irrelevant (mostly common
fixed cost) of the seller become relevant cost to the buyer.
3. Full Cost Plus. All manufacturing, selling and administrative cost plus a markup for profit. Standard cost plus would be better than actual cost plus to motivate the seller to be an efficient cost producer. The same problems in 2 are applicable here. Motivation for over allocation is still present. Transfers at standard could motivate the seller to rig the standard.
4. Variable cost. All variable manufacturing, selling and administrative cost. This may come close to accomplishing objective 3, since variable cost may approximate differential cost. It should be noted however, that variable cost and differential cost are not the same since some fixed cost may also be relevant, i.e., change if the product is purchased outside rather than produced inside. Objectives 1 and 2 would not be obtained since the other problems listed under 2 and 3 are applicable here, lack of motivation for profits, potential for cost over allocation etc.
5. Variable cost plus. This may be a little better than 4, but the plus should be kept separate to allow for a ball park make or buy decision. Objectives 1 and 2 would not be fully obtained.
6. Negotiated price. Negotiated prices may be best if:
a. An imperfect market exist for the product making it difficult, if not impossible, to determine the appropriate market price.
b. The seller has excess capacity, thus the transfer becomes a differential cost problem to the seller. Any transfer price above the seller's
differential cost would benefit the seller.
c. There is no external market for the product, thus no market price.
In these cases the buyer and seller may negotiate a price that allows both parties to share in the benefits of the transfer. This may accomplish objectives 1 and 2, but not 3. A problem with this approach is that managers may spend a substantial amount of time and effort negotiating transfer prices.
7. Dual Price. Use two transfer prices. Give the seller credit for selling at market price or full cost plus a reasonable markup, but charge the buyer with variable cost (i.e., approximate differential or additional outlay cost). Charge the difference to a central account. This approach may not motivate either the seller or the buyer to be efficient.
Very General Rule:
Optimum Price = Additional Outlay Cost + Opportunity Cost
Opportunity Cost = Market Price - Additional Outlay Cost
Opportunity Cost is the contribution margin that the seller would earn if the product could be sold on the outside market.
If the seller has excess capacity, i.e., cannot sell additional units on the outside market, then the seller's opportunity cost is zero. Thus, it is argued that the seller should transfer the product at cost. A problem may arise however, since the seller has no incentive to produce the extra product.
Maximum Price = Market Price
Minimum Price = Additional outlay cost, i.e., differential cost.
Transfer pricing is a classic catch-22 situation, a problem without a definitive answer.
Additional Problems with Multinational Transfer Pricing
1. Taxes rates in different countries.
The firm's strategy is to shift income from the high tax country to the low tax country. If the buying division is in a low tax country, then transfers would be made at the lowest cost possible. If the seller is in a low tax country transfers would be made at high prices.
2. Foreign Laws preventing income and dividend repatriations.
If there are restrictions on the buying division payments of dividends and transfers of income to the central office, then transfers of products to the buyer would be made at high prices. Transfers from the foreign division would be made a low prices.
Appendix 14-1: Conflict Between Choosing Capital Projects and Evaluating Results
The traditional recommended approach for choosing Capital Budgeting projects involves using discounted cash flow methods. These include the net present value method (NPV) and the internal rate of return (IRR). The IRR is the discount rate that makes the present value of the cash inflows from an investment equal to the present value of the cash outflows.
Frequently the IRR is used to choose projects and the ROI is used to evaluate performance. A conflict arises because the ROI (accounting rate of return) and IRR are different measurements. The IRR is an average time adjusted rate over the life of the project. The ROI is based on a single year and reflects returns based on conventional depreciation methods, i.e., usually net book value.
Possible Solutions To Conflict Between IRR and ROI
1. Use Compound Interest Depreciation. (Also called the Annuity Method.)
2. Use a Dual Planning Model.
Compound Interest Depreciation
Cash inflows are made up of two parts:
1. Interest Return = (Beginning Book Value)(IRR)
2. Depreciation = Recovery of Principal = Expected Cash Inflow - Interest Return from 1.
Example:
Cost of Project = $7,132. Two year life. Annual net cash inflow = $4,000.
IRR 8% ($7,132/4000 = 1.783)
Interest Return Year 1 = ($7,132)(.08) = $571.00
Depreciation Year 1 = $4,000 - 571 = $3,429.00
Interest Return Year 2 = ($7,132 - 3,429)(.08) = $296.24
Depreciation Year 2 = $4,000 - 296.24 = $3,703.76
Comparison of Compound Interest depreciation with Straight line and Sum-of-the-years-digits.
Assume actual cash flows are equal to expected cash flows.
|
Compound Interest |
Straight Line | Sum of the years digits |
||||
| Year 1 | Year 2 | Year 1 | Year 2 | Year 1 | Year 2 | |
| Actual Net Cash Inflow | $4,000 | $4,000 | $4,000 | $4,000 | $4,000 | $4,000 |
| Depreciation | 3,429 | 3,704 | 3,566 | 3,566 | 4,755 | 2,377 |
| Net Income | $571 | $296 | $434 | $434 | $(755) | $1,623 |
| ROI = NI ÷ Net Book Value | 571 7,132 = 8% |
296 3,704 = 8% |
434 7,132 = 6% |
434 3,566 = 12% |
(755) 7,132 = -11% |
1,623 2,377 = 68% |
Now assume that the actual net cash inflows are not equal to expected net cash inflows. Under the compound interest method, a net cash inflow in a given year that is different from the expected amount will cause the ROI to be different from the estimated IRR. For example, suppose the net cash inflow for year 2 above is $3,900. Under the compound interest method the ROI drops to 5.3%. The other depreciation methods do not provide this signal, i.e., that the internal rate of return is below the expected return.
|
Compound Interest |
Straight Line | Sum of the years digits |
||||
| Year 1 | Year 2 | Year 1 | Year 2 | Year 1 | Year 2 | |
| Actual Net Cash Inflow | $4,000 | $3,900 | $4,000 | $3,900 | $4,000 | $3,900 |
| Depreciation | 3,429 | 3,704 | 3,566 | 3,566 | 4,755 | 2,377 |
| Net Income | $571 | $196 | $434 | $334 | $(755) | $1,523 |
| ROI = NI ÷ Net Book Value | 571 7,132 = 8% |
196 3,704 = 5.3% |
434 7,132 = 6% |
334 3,566 = 9.4% |
(755 7,132 = -11% |
1,523 2,377 = 64% |
Why the Compound Interest Method is not used
1. The method is hard to understand and not consistent with external reporting.
2. The depreciation charge increases over the life of the asset. This seems to violate the matching concept.
3. There is a possibility of negative depreciation in some years.
The Dual Planning Model
Plan with the DCF model and evaluate with the accounting rate of return model. In other words, choose capital budgeting projects using the DCF methods (IRR and NPV), but restate the expected results in terms of the accounting rate of return (ROI). Then compare actual ROI with expected ROI to evaluate performance.
1 Johnson, H. T. and R. S. Kaplan. 1987. Relevance Lost: The Rise and Fall of Management Accounting. Boston: Harvard Business School Press. The graphic is adapted from Figure 4-1, page 85. (See the Summary of Chapter 4 for more on how Dupont used the ROI measurement).
2 See Read, R. B. 1954. Return on investment - A guide to management decisions. N.A.C.A. Bulletin (June): 1231-1244; Danfy, R. J. 1975. Analyzing the return on investment. Management Accounting (September): 31-32; and National Association of Accountants. Return on Capital as a Guide to Managerial Decisions. NAA Research Report No. 35: 33.
Appendix 14-2: What is input-output accounting?
Performance Measurements Main Page