Chapter 11
Conventional Linear Cost-Volume-Profit Analysis
James R. Martin, Ph.D., CMA
Professor Emeritus, University of South Florida
MAAW's Textbook Table of Contents
After you have read and studied this chapter, you should be able to:
1. Discuss the assumptions underlying the conventional linear cost-volume-profit
(CVP) model.
2. Explain the implications of relaxing each of these assumptions in terms of
the theoretical cost- volume-profit model.
3. Explain the meaning of a series of graphic illustrations for both the
linear and nonlinear CVP models including production functions, revenue
functions and cost functions.
4. Discuss the difference between performing a "what-if" analysis
and converting from the linear model to the theoretical nonlinear model.
5. Solve a variety of linear CVP problems for single product companies in
either units or sales dollars.
6. Define and use the margin of safety.
7. Solve a variety of linear CVP problems for multiproduct companies in
either units or sales dollars.
8. Solve similar problems on a cash flow basis.
9. Discuss the controversy concerning the compatibility of the contribution
margin approach with activity based costing and the lean enterprise concepts of just in time and
the theory of constraints.
Conceptually, conventional linear cost-volume-profit (CVP) analysis is a simplified, short term planning technique that evolved as a practical version of the theoretical model of the firm described in economics textbooks.1 From an accounting perspective it is compatible with the direct, or variable costing method of inventory valuation. To use the CVP model, a company must separate total costs into fixed and variable categories using one of the methods described in Chapter 3. Recall from our earlier discussions of these terms that variable costs are those costs that vary with changes in the level of activity. The only activities that are allowed to affect variable costs in traditional cost-volume-profit analysis are production output and sales. Remember that fixed costs are those costs that do not vary with changes in the activity level. Conceptually, fixed costs are not constant. By definition, fixed simply means that these costs are not driven by short run changes in production or sales volume. Although explicit recognition of non production volume related cost drivers is a key concept in activity based costing, the idea is ignored in the conventional linear CVP model.2 Finally, it is important to recognize that the concept of fixed and variable costs is a short run concept. All costs tend to vary in the long run as the company adds to its' capacity to produce and distribute products and services. Therefore, the short run emphasis of CVP analysis tends to conflict with the long run emphasis of activity based costing and the lean enterprise concepts of JIT and TOC. This creates another thought provoking controversial issue.
The purpose of this chapter is to describe the assumptions and techniques of the conventional linear cost-volume-profit approach as well as the controversy concerning the compatibility of CVP analysis with ABC and the continuous improvement concepts. The chapter is divided into five main sections. The first section addresses the underlying assumptions of the conventional linear model and the implications of relaxing these assumptions. This section is mainly conceptual and is illustrated with a series of graphs. The second section illustrates the basic planning techniques for a single product company that provide the foundation for more realistic problems. The third section extends the basic analysis to multiproduct companies. Both sections two and three are more mechanical than conceptual and are mainly illustrated with a series of related equations. The fourth section is fairly short, but illustrates how to convert the analysis to a cash flow basis. The last section introduces the controversy associated with the CVP approach as it relates to the newer concepts of ABC, JIT and TOC. Since the CVP methodology is closely related to direct or variable costing, this chapter helps provide a better foundation for the more detailed comparison of direct and absorption costing presented in Chapter 12.
ASSUMPTIONS OF CONVENTIONAL LINEAR CVP ANALYSIS
Conventional linear cost volume profit analysis is based on five assumptions as follows:
1. Constant sales price.
2. Constant variable cost per unit.
3. Constant total fixed cost.
4. Constant sales mix.
5. Units sold equal units produced.
Note that these are the same assumptions that are applicable to the master budget, with the exception of number five. Now we will examine the implications of each assumption.
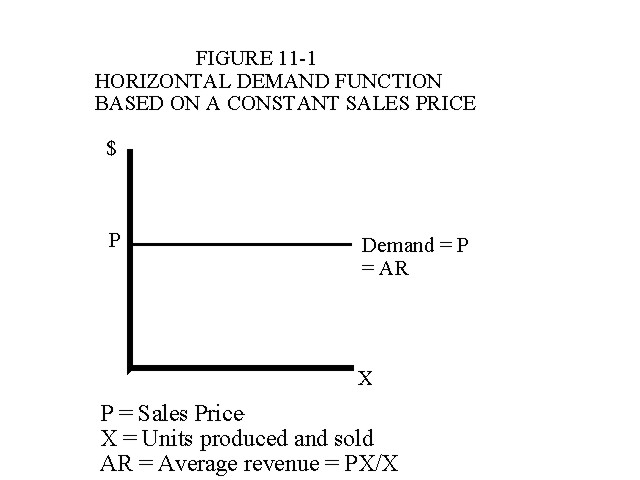
To assume that the sales price is constant implies that the company is facing a horizontal demand function as illustrated in Figure 11-1. The implications of a horizontal demand function are that the company can sell any number of units at a constant sales price. Another way to describe this is to say that consumers are willing and able to buy any quantity the company offers for sale at a constant price. Average revenue (AR) is constant and equal to the sales price, (i.e., AR = PX÷X = P) as illustrated in Figure 11-1.
The slope of the total revenue function (see Figure 11-2) is equal to the sales price. When the company sells one additional unit, total revenue increases by an amount equal to the sales price of that unit. The fact that the sales price is constant causes the slope of the total revenue function to be constant which results in a linear total revenue function. Another way to describe this is to say that total revenue increases at a constant rate as additional units are sold.
A more realistic down sloping demand function (see Figure 11-3) illustrates what economists refer to as the law of demand. This law describes the fundamental idea that consumers are willing and able to buy more at a lower price than a higher price. When the price is decreased from P1 to P2, the quantity purchased, or demanded, increases from X1 to X2. The total revenue function based on the law of demand is nonlinear as illustrated in Figure 11-4. Total revenue increases at a decreasing rate as additional units are sold. This is because the sale of additional units requires that the company reduce the sales price. Each price corresponds to a specific sales quantity. Thus, average revenue (AR) will be decreasing, rather than constant.
Although the assumption of a constant sales price is not realistic, it is defended as a practical way to expedite the planning process within a fairly narrow range of sales activity. The idea that most products are subject to a down sloping demand curve is intuitively obvious, but applying the concept is simply not practical. Most companies sell too many products in a constantly changing economic environment. Today’s demand curve is very likely to be obsolete tomorrow.
Constant Variable cost per unit
The second assumption of the conventional linear cost-volume-profit approach is that the variable cost per unit of output is constant. This includes two important underlying assumptions: a) input prices are assumed to be constant for all variable inputs such as direct material, direct labor, and the various types of indirect resources represented by variable factory overhead costs and variable selling and administrative expenses, and b) the firm experiences constant productivity, i.e., constant output per variable input. Constant productivity is illustrated in Figure 11-5. When productivity is constant, each new unit of output requires an equal amount of input and thus each unit of output will cost the same amount. This causes both the production function to be linear (see Figure 11-5) and the average variable cost function to be horizontal (see Figure 11-6). Output (X) is placed on the vertical axis in Figure 11-5 because output is the dependent variable, i.e., inputs drive outputs. Output is on the horizontal axis in the other graphs because cost is the dependent variable, i.e., output drives cost.
Although it is convenient to assume constant productivity for short run planning purposes, other types of production functions are more realistic when the whole range of production possibilities is considered. When a company begins to expand output from a low volume startup level to a medium volume level, productivity might be expected to increase due to the effects of increased specialization, experience and learning. When productivity is increasing, output increases at an increasing rate (see Figure 11-7). As variable inputs are added to production, each input generates more output than the previous input. When productivity is increasing, average variable cost per unit will be decreasing as in Figure 11-8.
If the company increased production from a medium volume level to a high volume level by continuing to add variable inputs to a fixed size facility, productivity would be expected to decrease as indicated in Figure 11-9. This is because at high volume production levels, the inputs (labor, materials etc.) would become excessive relative to the size of the fixed facility. In the case of decreasing productivity, average variable cost per unit will be increasing as illustrated in Figure 11-10. Each unit will cost more because it requires more inputs to produce.
Theoretically, the production and average variable cost functions for the entire range of short run production possibilities will be similar to those illustrated in Figures 11-11 and 11-12. The point where the production function changes directions from increasing to decreasing productivity and the average variable cost function changes from decreasing to increasing cost per unit is referred to as the point of diminishing returns. Output continues to increase beyond this point, but at a decreasing rate.
Constant Fixed Costs and The Families of Total Cost Functions
A family of total cost functions for the conventional linear model is presented in Figure 11-13. The total variable cost and total cost functions are linear, i.e., they increase at a constant rate, because productivity is assumed to be constant. The total fixed cost function is represented by a horizontal line because of assumption three which eliminates the possibility of a non-output related change in fixed costs during the planning period. No changes in the company’s fixed factors of production can occur. The total cost and total variable cost functions are vertically parallel and separated by the amount of total fixed costs.
A comparable family of total cost functions for the theoretical economic model appears in Figure 11-14. The total variable cost and total cost functions increase at a decreasing rate at first in response to increasing productivity. When the inputs are becoming more productive, additional outputs cost less per unit because they require less input. However, when productivity begins to decrease, the total cost and total variable cost functions begin to increase at an increasing rate. In the case of decreasing productivity, the inputs are generating less output per input, thus the unit cost of additional outputs is increasing. The total cost functions in Figure 11-14 are also parallel and separated vertically by the amount of total fixed costs.
Constant Sales Mix and Inventory Level
The last two assumptions of the conventional linear cost-volume-profit model are more easily understood than the previous assumptions. The fourth assumption is that the sales mix will remain constant during the planning period for a multiproduct company. Sales mix proportions may be stated in terms of either units or dollars as explained in the illustrations below.
The fifth and last assumption is that units produced are equal to units sold. This means that there will be no changes in beginning or ending inventory levels to complicate the analysis. This assumption along with the assumption concerning constant fixed cost will be relaxed in the following chapter where we will use the conventional linear CVP model to consider the differences between direct costing and full absorption costing.
Summary of the Conventional Linear and Theoretical Models
Graphic summaries of the two models are presented in Figures 11-15 and 11-16. In the linear model there is one break-even point (BEP) where total revenue is equal to total cost. Since the total revenue and total cost functions are linear, the profit function is also linear. This is because the slope of the profit function is equal to contribution margin per unit which is automatically constant when the sales price and variable cost per unit are constant.
The theoretical model summarized in Figure 11-16 conveys a very different picture. There are two break-even points where total revenue and total cost are equal. The theoretical profit function intersects the horizonal axis at the two break-even points and reaches a maximum level at the point where the vertical distance between TR and TC is the greatest. In the linear model illustrated in Figure 11-15, the area to the left of the break-even point represents a loss area and the area to the right of this point represents a profit area that continuously grows larger as additional units are produced and sold. In the linear model the company maximizes profit where production and sales are at maximum capacity. However, in the theoretical model , there are two loss areas, one to the left of the first BEP and one to the right of the second BEP. The profit area is between the two break-even points, thus trying to achieve the maximum level of production and sales will produce losses rather than increased profits.3 For this reason, some critics of the conventional linear model argue that it represents a naive and dangerous view of a firm's economic environment. On the other hand, advocates of the linear model contend that short term planning does not require a theoretical model of the entire range of production possibilities. Although the concepts underlying the theoretical model are important, the model does not provide a practical approach for short term planning. However, the linear model is a practical and adequate alternative for planning within the normal relevant range of production and sales alternatives.
"What-If" Analysis Versus Changing the Model
For any given linear CVP analysis, we can ask a whole set of "what-if" questions about how increases and decreases in the sales price, unit variable costs, sales mix and fixed costs would affect the outcome. However, when we do that we are simply changing from one set of static assumptions to another set. This means that we are changing from one conventional linear problem to a somewhat different conventional linear problem. If the first two assumptions are relaxed to allow the sales price and unit variable costs to change continuously in response to the forces of supply and demand, we are not asking a "what if" question, we are changing the analysis from the practical linear approach to the theoretical nonlinear approach.
TECHNIQUES FOR SOLVING CVP PROBLEMS
The following symbols are used below to illustrate the various techniques used in cost-volume-profit analysis.
P = Sales price.
V = Variable costs per unit. Note: This is not inventory cost
because it includes both variable manufacturing costs as
well as variable selling and administrative expenses.
X = The number of units produced and sold. A unit is a common
way to describe an output, but an output may be expressed
in pounds, gallons, board feet, cubic feet, etc.
TR = S = Total revenue, or sales dollars.
TVC = Total variable costs = VX
TFC = Total fixed costs.
TC = Total costs = TFC + TVC.
P-V = Contribution margin per unit. This is the amount of
sales revenue that each unit provides towards covering the
fixed costs and providing a profit, i.e., what's left over after
the variable costs associated with the unit have been covered.
TCM = Total contribution margin = (P-V)(X).
CMR = (P-V)÷P = (TR-TVC)÷TR = (PX-VX)÷PX = 1-(V÷P). These
are just different ways to define the contribution margin
ratio. They all work because the functions are linear.
There are many algebraic equations illustrated on the next several pages that may appear to require memorization. However, every equation is simply a variation of the following basic concepts:
Total Revenue = Total Cost + Profit
TR = TC + NIBT
TR = TFC + TVC + NIBT
TR - TVC = TFC + NIBT
TCM = TFC + NIBT
Total revenue, or sales dollars, less total variable costs equals total contribution margin. Contribution margin is the revenue over and above the variable costs that contributes towards covering the fixed costs and also towards providing a profit after the fixed costs have been covered. Practically any cost-volume-profit problem can be solved with the last equation stated above and an understanding of the concepts involved.
SOLVING SINGLE PRODUCT CVP PROBLEMS IN UNITS
A summary of the cost volume profit equations for single product problems is presented in Exhibit 11-1. All five equations are variations of the basic conceptual equation stated above. To reinforce the concept, each equation is developed and illustrated below.
|
EXHIBIT 11-1 SUMMARY EQUATIONS FOR SOLVING SINGLE PRODUCT CVP PROBLEMS IN UNITS |
||
| Number | Equation | Used to Determine |
| [1] | (P-V)X = TFC | Units needed to break-even. |
| [2] | (P-V)X = TFC + NIBT | Units needed to generate a target net income before taxes. |
| [3] | (P-V)X = TFC + [NIAT ÷ (1-T)] | Units needed to generate a target net income after taxes. |
| [4] | (P-V)X = TFC + (R)(PX) | Units needed to generate a target NIBT stated as a proportion (R) of sales dollars (PX). |
| [5] | (P-V)X = TFC + [(R)(PX) ÷ (1-T)] | Units needed to generate a target NIAT stated as a proportion (R) of sales dollars (PX). |
UNITS NEEDED TO BREAK-EVEN
We can derive the break-even equation by starting with the fact that total revenue equals total cost at the break-even point. Then the equation is restated in terms of unit sales, unit prices and unit cost and then rearranged into the more convenient format presented in Equation 1.
TR = TC
TR = TFC + TVC
PX = TFC + VX
PX - VX = TFC
[1] (P-V)X = TFC or TCM = TFC
X = TFC ÷ (P-V)
Equation 1 shows that the break-even point is where total contribution margin (P-V)(X) is equal to total fixed costs, i.e., this level of production and sales provides just enough revenue to cover all the cost.
UNITS NEEDED FOR TARGET NET INCOME BEFORE TAXES
This equation can be derived from scratch in the same manner used to develop Equation 1. Notice however that Equation 2 may be obtained by simply adding the desired amount of net income to the right hand side of Equation 1.
TR = TFC + TVC + TARGET NIBT
PX = TFC + VX + NIBT
PX - VX = TFC + NIBT
[2] (P-V)X = TFC + NIBT
X = (TFC+NIBT) ÷ (P-V)
Equation 2 simply indicates that total contribution margin is equal to the total fixed costs plus the desired net income before taxes. These relationships are illustrated graphically in Figure 11-17 which is similar to Figure 11-15 presented in the previous section.
Figure 11-17 shows that the break-even point is where the two lines representing total revenue and total cost intersect. To the left of this intersection, the vertical difference between the total revenue and total cost functions represents a net loss. To the right of the break-even point, the vertical difference between the two functions represents net income before taxes. The lower part of the graph shows that the break-even point can also be found by plotting the before tax profit function. When the number of units produced and sold equals zero, the loss is equal to total fixed costs. When the firm produces a positive number of units, the loss is reduced by an amount equal to the contribution margin per unit multiplied by the number of units produced and sold. The slope of NIBT is contribution margin per unit. When enough units are produced and sold to cover the fixed costs, the company reaches the break-even point. This is the point on the graph where the profit function intersects the horizontal axis and it is directly below the point where the total revenue and total cost functions intersect.
UNITS NEEDED FOR TARGET NET INCOME AFTER TAXES
If T = the tax rate, and NIAT = desired net income after taxes, then
(1-T)(NIBT) = NIAT therefore NIBT = NIAT ÷ (1-T)
Substituting NIAT÷(1-T) for NIBT in Equation 2, provides Equation 3, which allows us to solve for units needed to generate a desired amount of net income after taxes.
[3] (P-V) X = TFC + [NIAT ÷ (1-T)]
X = [TFC + [NIAT÷(1-T)]] ÷ (P-V)
The after tax relationships are also illustrated graphically in Figure 11-17. The after tax profit function begins at a point equal to (1-T)(-TFC) assuming the tax benefits of a loss can be used in a prior period or perhaps in some other segment of the company. The slope of the after tax profit function is (1-T)(P-V), therefore the function is not as steep as the before tax profit function. The break-even point is the same however, and the vertical difference between the two profit functions is equal to the amount of the tax involved.
WHEN TARGET NET INCOME BEFORE TAXES IS STATED AS A % OF SALES $
If we use R to define the desired rate of return on sales, i.e., R = NIBT/TR, then we can substitute R(PX) for the desired net income before taxes in Equation 3. This provides Equation 4.
[4] (P-V)X = TFC + (R)(PX)
X = [TFC + (R)(PX)] ÷ (P-V)
Since PX equals sales dollars, then R multiplied by PX will provide the desired profit before taxes.
Although the desired profit is often stated as a percentage, R is a proportion, i.e, it ranges from 0 to 1.
WHEN TARGET NET INCOME AFTER TAXES IS STATED AS A PERCENTAGE OF SALES $
If the target rate of return is stated as an after tax rate, i.e., R = NIAT/TR, then the following approach is used. Substituting R(PX)÷(1-T) for R(PX) in Equation 4 provides Equation 5.
[5] (P-V)X = TFC + [(R)(PX) ÷ (1-T)]
X = [TFC + [(R)(PX) ÷ (1-T)]] ÷ (P-V)
When solving CVP problems, it is less confusing visually and more convenient for computational purposes to leave (P-V) on the left-hand side of the equations initially as indicated in Exhibit 11-1. It is best to simplify the expressions on both sides of the equation first, rather than attempt to divide every element on the right-hand side by P-V.
The Cal Company produces pocket size calculators that are sold for $10 per unit. The costs associated with each unit are as follows: Direct material = $3.00, Direct labor = $ .25, Variable overhead = $2.00, and Variable selling and administrative cost = $ .75. Total fixed costs are $100,000 for manufacturing and $20,000 for the selling and administrative functions. The company’s tax rate is 40%.
In a recent meeting, the board of directors asked the following questions. How many calculators do we need to produce and sell to accomplish each of the following requirements? 1. Break-even. 2. Earn net income before taxes of $40,000. 3. Earn net income after taxes of $24,000. 4. Earn a 20% return on sales before taxes. 5. Earn a 12% return on sales after taxes.
To answer these questions, we start by calculating the contribution per unit as follows: Contribution margin per unit = P - V = 10 - (3 + .25 + 2 + .75) = 10 - 6 = 4. Then, the five questions are answered by using the equations in Exhibit 11-1.
1. Break-even
Using Equation [1] 4X = 120,000
X = $120,000 ÷ 4 = 30,000 units
2. Earn net income before taxes of $40,000
Using Equation [2] 4X = 120,000 + 40,000
X = 160,000 ÷ 4 = 40,000 units.
3. Earn net income after taxes of $24,000
Using Equation [3] 4X = 120,000 + [24,000 ÷ (1-.4)]
4X = 120,000 + 40,000
X = 160,000 ÷ 4 = 40,000 unit.
A graphic solution to Example 11-1 is illustrated in Figure 11-18.
4. Earn a 20% return on sales before taxes
Using Equation [4] 4X = 120,000 + .2(10X)
4X = 120,000 + 2X
2X = 120,000
X = 120,000 ÷ 2 = 60,000 units
5. Earn a 12% return on sales after taxes
Using Equation [5] 4X = 120,000 + [.12(10X) ÷ (1-.4)]
4X = 120,000 + .2(10X)
4X = 120,000 + 2X
2X = 120,000
X = 120,000 ÷ 2 = 60,000 units
Using The After Tax Equations As An Alternative
The equation for NIAT that appears in the graph is found by multiplying the equation for NIBT by (1-T) , i.e., (1-.4)(-120,000 + 4X) = -72,000 + 2.4X. Rearranging this equation we have 2.4X = 72,000 + NIAT. This revised equation indicates that the contribution margin after taxes ($2.4X) is equal to fixed costs after taxes ($72,000) plus the desired after tax income. It provides an alternative way to find the answers to questions 3 and 5 as illustrated below.
3. Earn net income after taxes of $24,000
2.4X = 72,000 + NIAT desired
2.4X = 72,000 + 24,000
2.4X = 96,000
X = 96,000 ÷ 2.4 = 40,000 units.
5. Earn a 12% return on sales after taxes
2.4X = 72,000 + NIAT desired
2.4X = 72,000 + .12(10X)
2.4X = 72,000 + 1.2X
1.2X = 72,000
X = 72,000 ÷ 1.2 = 60,000 units.
Checking the Solutions
The accuracy of linear cost-volume-profit calculations can be verified easily. For example, the answers to the questions above can be verified as follows:
1) Is 30,000 units the break-even point? Yes, since total contribution margin is equal to total fixed cost of 120,000, i.e., (4)(30,000) = $120,000. 2) Will 40,000 units generate a before tax profit of $40,000? Yes, because total contribution margin is (4)(40,000) = $160,000 and this amount is 160,000 - 120,000 = $40,000 above total fixed costs. 3) Will 40,000 units generate an after tax profit of $24,000? Yes, since (1-.4)($40,000 NIBT) = $24,000. 4) Will 60,000 units provide a 20% return on sales before taxes? Yes, since the NIBT is TCM - TFC or (4)(60,000) - 120,000 = $120,000. Sales equals PX or ($10)(60,000) = $600,000. R = 120,000 ÷ 600,000 = .20 or 20%. 5) Will 60,000 units provide a 12% return on sales after taxes. Yes, (1-.4)(.2) = .12 or 12%. For an alternative check (1-.4)(120,000) = $72,000 NIAT. Therefore, the after tax rate of return is 72,000 ÷ 600,000 = .12 or 12%.
SOLVING SINGLE PRODUCT CVP PROBLEMS IN DOLLARS
A summary of the cost volume profit equations for solving single product problems in dollars is presented in Exhibit 11-2. These five equations are also variations of the basic conceptual equation stated in the first part of this chapter. Each of these equations is developed and illustrated below.
|
EXHIBIT 11-2 SUMMARY EQUATIONS FOR SOLVING SINGLE PRODUCT CVP PROBLEMS IN DOLLARS |
||
| Number | Equation | Used to Determine |
| [1] | (CMR)(S) = TFC | Sales $ at break-even point |
| [2] | (CMR)(S) = TFC + NIBT | Sales $ for target NIBT |
| [3] | (CMR)(S) = TFC + [NIAT ÷ (1-T)] | Sales $ for target NIAT |
| [4] | (CMR)(S) = TFC + (R)(S) | Sales $ for target NIBT stated as a proportion (R) or sales $ |
| [5] | (CMR)(S) = TFC + [(R)(S) ÷ (1-T)] | Sales $ for target NIAT stated as a proportion (R) of sales $ |
BREAK-EVEN POINT IN DOLLARS FOR A SINGLE PRODUCT
The equation for the break-even point in sales dollars may also be derived by equating total revenue and total cost. It is more convenient to use the single symbol S for sales dollars, rather than TR for total revenue.
TR = TC
S = TFC + TVC
Since the variable cost ratio (V÷P) multiplied by sales dollars (S) equals total variable cost, we can substitute (V÷P)(S) for variable cost in the equation above as follows.
S = TFC + (V÷P)(S)
Then subtracting variable cost from both sides of the equation provides the basic break-even point equation in sales dollars.
S - (V÷P)(S) = TFC
Stated in words, the equation indicates that total revenue, less total variable costs, equals total contribution margin, and the break even point is where total contribution margin is equal to total fixed cost. Since the contribution margin ratio (CMR = 1- V÷P) multiplied by total revenue equals total contribution margin, it is more convenient for computational purposes to state the equation in the following manner.
(1- V÷P)(S) = TFC
[1] (CMR)(S) = TFC
S = TFC ÷ CMR
TOTAL REVENUE NEEDED FOR TARGET NET INCOME BEFORE TAXES
Although we could derive this equation from scratch, the fact that total contribution margin must be equal to the total fixed costs plus the desired net income before taxes allows us to develop Equation 2 by simply adding the desired net income to Equation 1.
[2] (CMR)(S) = TFC + NIBT
S = (TFC+NIBT) ÷ CMR
TOTAL REVENUE NEEDED FOR TARGET NET INCOME AFTER TAXES
Solving for total revenue needed to generate a target net income after taxes involves substituting NIAT ÷ (1-T) for NIBT in the equation for Sales dollars needed before taxes (i.e., Equation 2). This provides Equation 3.
[3] (CMR)(S) = TFC + [NIAT ÷ (1-T)]
S = [TFC + [NIAT ÷ (1-T)]] ÷ CMR
TOTAL REVENUE NEEDED WHEN TARGET NIBT IS STATED AS A PERCENTAGE OF SALES $
To solve a problem in sales dollars, when the desired net income is stated as a percentage of sales dollars, substitute (R)(S) into Equation 2 for NIBT as follows.
[4] (CMR)(S) = TFC + (R)(S)
S = [TFC + (R)(S)] ÷ CMR
TOTAL REVENUE NEEDED WHEN TARGET NIAT IS STATED AS A PERCENTAGE OF SALES $
When the desired net income is stated as an after tax rate (R), the equation needed is developed by simply dividing (R)(S) in Equation 4 by (1-T).
[5] (CMR)(S) = TFC + [(R)(S) ÷ (1-T)]
S = [TFC + [(R)(S) ÷ (1-T)]] ÷ CMR
To emphasize a point made earlier, it is less confusing visually and also more convenient for computational purposes to leave CMR on the left-hand side of each of the 5 equations initially. Simplify the expressions first, rather than attempting to divide every element on the right-hand side by CMR.
EXAMPLE 11-2
The Cal Company example can be restated in the following manner. Variable costs (including both manufacturing and selling and administrative costs) represent sixty percent of sales dollars. Total fixed costs are $120,000.
Assume the board of directors wants the answers to their questions provided in sales dollars rather than units. What amount of sales in dollars does the company need to accomplish each of the following requirements? 1. Break-even. 2. Earn net income before taxes of $40,000. 3. Earn net income after taxes of $24,000. 4. Earn a 20% return on sales before taxes. 5. Earn a 12% return on sales after taxes. To answer these questions, we need the contribution margin ratio. The ratio is CMR = 1- V/P = 1-.6 = .4 Then, the answers to the five questions are easily obtained as follows:
1. Break even
Using Equation [1] .4S = 120,000
S = 120,000 ÷ .4 = $300,000
2. Earn net income before taxes of $40,000
Using Equation [2] .4S = (120,000 + 40,000)
S = 160,000 ÷ .4 = $400,000
3. Earn net income after taxes of $24,000
Using Equation [3] .4S = 120,000 + (24,000 ÷ .60)
.4S = 120,000 + 40,000
S = 160,000 ÷ .4 = $400,000
4. Earn a 20% return on sales before taxes
Using equation [4] .4S = 120,000 + .2S
.2S = 120,000
S = 120,000 ÷ .2 =
$600,000
5. Earn a 12% return on sales after taxes
Using equation [5] .4S = 120,000 + (.12S ÷ .6)
.4S = 120,000 + .2S
.2S = 120,000
S = 120,000 ÷ .2 = $600,000
A graphic analysis of this example is also illustrated in Figure 11-18 since we are simply solving the problem in dollars rather than units. The graph is also useful for comparing the two approaches. Example 11-1 places emphasis on the horizontal axis (units) while Example 11-2 places emphasis on the vertical axis ( dollars).
Before we move on to multiproduct companies, there is a handy concept referred to as the margin of safety that you might find useful. The margin of safety (MS) for any sales level represents the amount of sales dollars above or below the break-even point. Mathematically, the margin of safety is:
MS = Sales$ - Break-even sales$
When sales are above the break-even point, the margin of safety is positive. When sales are below the break-even point, the margin of safety is negative. After determining the MS for a particular sales level, Equations 6 and 7 can be used to make some quick calculations.
[6] NIBT = (MS)(CMR)
Solving Equation 6 provides the amount of contribution margin above the break-even point (when MS is positive) and this amount represents the net income (or loss if the MS is negative) before taxes. Why? Because after the total fixed costs have been covered, additional contribution margin represents the before tax profit. Before the fixed cost have been covered the additional contribution needed represents the before tax loss.
The equation for after tax profit is
[7] NIAT = (MS)(CMR)(1-T)
EXAMPLE 11-3
Suppose we are in a board of directors meeting and a board member asks how much income would Cal Company generate at a particular sales level. For convenience let’s say $1,000,000. Using the margin of safety we can answer this question quickly. Since we already know the break-even point is $300,000, then the margin of safety is 1,000,000 - 300,000 = $700,000.
Using Equation [6] NIBT = (700,000)(.4) = $280,000.
Using Equation [7] NIAT = (700,000)(.4)(.6) = $168,000.
To show that the margin of safety calculations work on either side of the break-even point, consider another example. Suppose someone ask, how much income would Cal Company generate when total revenue is only $200,000?
MS = 200,000 - 300,000 = -100,000, i.e., $100,000 below the BEP.
Using Equation [6] NIBT = (-100,000)(.4) = -40,000 net loss before taxes, or
Using Equation [7] NIAT = (-40,000)(.6) = -24,000 net loss after taxes.
SOLVING MULTIPLE PRODUCT CVP PROBLEMS IN UNITS
Some additional symbols are needed to illustrate the algebraic techniques applicable to multiple product problems.
The following symbols are used below:
i = The number designating a particular product.
Pi = The price of product i.
Vi = The variable cost per unit of product i.
X = Total mixed units sold, i.e., includes all products.
Xi = Units of product i sold.
Mi = The mix ratio for product i, i.e., the proportion that product i represents out of the total number of units sold.
∑ = Sigma or summation sign which means "the sum of".
W = Weighted average contribution margin per unit = ∑ [(Pi-Vi)(Mi)]
Y = The weighted average price = ∑ (Pi)(Mi)
A summary of the cost volume profit relationships for multiproduct problems is presented in Exhibit 11-3. The five equations are comparable to the single product equations presented in Exhibit 11-1, but are somewhat more involved. Each equation is developed and illustrated below
|
EXHIBIT 11-3 SUMMARY EQUATIONS FOR SOLVING MULTIPLE PRODUCT CVP PROBLEMS IN UNITS |
||
| Number | Equation | Used to Determine |
| [1] | WX = TFC | Total mixed units at the BEP. |
| [2] | WX = TFC + NIBT | Total mixed units for target NIBT. |
| [3] | WX = TFC + [NIAT ÷ (1-T)] | Total mixed units for target NIAT. |
| [4] | WX = TFC + (R)(YX) | Total mixed units for target NIBT stated as a proportion (R) of sales $. |
| [5] | WX = TFC + [(R)(YX) ÷ (1-T)] | Total mixed units for target NIAT stated as a proportion (R) of sales $. |
| Xi = X(Mi) | The number of units of each product after X is obtained. | |
BREAK-EVEN POINT IN UNITS FOR MULTIPLE PRODUCTS
The same logic used to solve single product problems is applicable to multiple product problems. At the break-even point, total contribution margin is equal to total fixed costs. However, in multiple product situations, total contribution margin is found by multiplying the weighted average contribution margin per unit by the total number of mixed units produced and sold. The weighted average contribution margin per unit is calculated by multiplying each product's contribution margin per unit (Pi-Vi) by the mix ratio applicable to that product (Mi) and then summing the results. The mix ratios (Mi's) represent the weights. The equation is,
W = ∑ [(Pi-Vi)(Mi)]
The break-even equation for mixed units (X) is stated in the following manner.
[1] WX = TFC
After the total mixed units (X) have been determined, then the number of units of the individual products are found by multiplying the total mixed units by each product's mix ratio.
Xi = X(Mi)
UNITS NEEDED FOR TARGET NET INCOME BEFORE TAXES
The equation for mixed units needed to generate a desired amount of net income before taxes is developed by simply adding NIBT to the right hand side of Equation 1.
[2] WX = TFC + NIBT
UNITS NEEDED FOR TARGET NET INCOME AFTER TAXES
The equation for mixed units needed to generate a desired after tax profit is developed by substituting NIAT ÷ (1-T) for NIBT in Equation 2.
[3] WX = TFC + [NIAT ÷ (1-T)]
WHEN TARGET NET INCOME BEFORE TAXES IS STATED AS A PERCENTAGE OF SALES $
Using R to represent the target rate of return on sale dollars before taxes, i.e., R = NIBT÷TR, the following equation can be used to find the mixed units needed.
[4] WX = TFC + (R)(YX)
Sales dollars are represented by the term YX. Since total sales dollars are mixed, we must multiply the total mixed units (X) by a weighted average price (Y) to find the total mixed sales dollars. Then, multiplying the term YX by R represents the desired NIBT. The weighted average price (Y) is found by multiplying the price of each product (Pi) by the product mix ratios (Mi) and then summing the results, i.e., Y = ∑(Pi)(Mi).
WHEN TARGET NET INCOME AFTER TAXES IS STATED AS A PERCENTAGE OF SALES $
The appropriate equation for after tax net income is found by dividing the term [(R)(YX], in Equation 4, by 1-T.
[5] WX = TFC + [(R)(YX) ÷ (1-T)]
Remember that it is usually best for computational purposes to leave the amount represented by W on the left hand side in each of the equations until the expression on the right hand side has been simplified. Also remember that the units for individual products (Xi) are always found by multiplying the total mixed units (X) by the mix ratios (Mi) for each product.
The Sandlot Cap Company produces baseball caps in two categories referred to as regular logo and special logo. Caps in the regular logo category are high volume products that display familiar names of universities and professional sports teams. Caps in the special design category are typically created for a particular customer to promote special events such as the Olympics, or the opening of a unique museum exhibit. For convenience we will refer to the regular logo caps as product X1 and the special logo caps as product X2. Sales prices and variable costs are provided below.
| Product | Price | Variable Cost Per Unit | Mix
Ratio Based on Units |
| X1 X2 |
$4 8 |
$3 5 |
.75 .25 |
The variable costs for each product include direct materials and conversion costs of $2. Marketing costs account for an additional $1 for regular logo caps and $3 for special logo caps. As indicated above, three quarters of the company’s unit sales are represented by regular logo caps, while the other one quarter represents special logo caps. The company’s total fixed costs are $300,000. Sandlot Cap Company management wants to know how many caps need to be produced and sold to accomplish the following:
1. Break even.
2. Earn desired net income before taxes of $60,000.
3. Earn desired net income after taxes of $36,000 given the tax rate is 40%.
4. Earn desired net income before taxes equal to 15% of sales dollars.
5. Earn a desired net income after taxes equal to 9% of sales dollars.
To solve this problem we need to calculate the weighted average contribution margin per unit, i.e., the contribution margin per mixed unit.
W = (4-3)(.75) + (8-5)(.25) = 1.5
The mix ratios (.75 and .25) are used as the weights to reflect the fact that the company normally sells three times as many X1's as X2's. After obtaining the weighted average contribution of $1.50, then 1.5X represents the total contribution margin on the lefthand side of each equation.
1. To break-even
Using Equation [1] 1.5X = 300,000
X = 300,000 ÷ 1.5 = 200,000 Total mixed units.
X1 = (200,000)(.75) = 150,000 units
X2 = (200,000)(.25) = 50,000 units
2. To earn $60,000 net income before taxes
Using Equation [2] 1.5X = 300,000 + 60,000
1.5X = 360,000
X = 360,000 ÷1.5 = 240,000 mixed units
X1 = (240,000)(.75) = 180,000 units
X2 = (240,000)(.25) = 60,000 units
3. To earn $36,000 net income after taxes
Using Equation [3] 1.5X = 300,000 + (36,000 ÷ .6)
1.5X = 300,000 + 60,000
X = 360,000 ÷1.5 = 240,000 mixed units
X1 = (240,000)(.75) = 180,000 units
X2 = (240,000)(.25) = 60,000 units
In the last two requirements, income is stated as a percentage of sales dollars. Therefore, we need the YX measure of total mixed sales dollars to indicate the desired amount of income. Total mixed sales dollars is the weighted average price Y, multiplied by the mixed units X. To calculate Y we must use the unit mix ratios as weights to reflect the importance of each product in the price.
Y = 4(.75) + 8(.25) = $5
Then, $5 represents the weighted average price and 5X represents the total mixed sales dollars.
4. To earn before tax net income equal to 15% of sales dollars, we substitute .15(5X) in the equation for desired income, i.e., R(YX)
Then using Equation [4]
1.5X = 300,000 + .15(5X)
1.5X = 300,000 + .75X
.75X = 300,000
X = 300,000 ÷ .75 = 400,000 mixed units
X1 = .75(400,000) = 300,000 units
X2 = .25(400,000) = 100,000 units
5. To earn after tax net income equal to 9% of sales dollars, the desired income is (R)(YX) ÷ 1-T, or (.09)(5X) ÷ (1-.4)
Then using Equation [5]
1.5X = 300,000 + [(.09)(5X) ÷ (1-.4)]
1.5X = 300,000 + [.45X ÷ .6]
1.5X = 300,000 + .75X
.75X = 300,000
X = 300,000 ÷ .75 = 400,000 mixed units
X1 = .75(400,000) = 300,000 units
X2 = .25(400,000) = 100,000 units
Using The After Tax Equations As An Alternative
A graphic analysis of the Sandlot Cap Company example appears in Figure 11-19.
The equation for NIAT illustrated in the graph is found by multiplying the equation for NIBT by (1-T), i.e., (1-.4)(-300,000) + (1-.4)(1.5X) = -180,000 + .9X. Rearranging this equation we have .9X = 180,000 + NIAT where .9X is the weighted average contribution margin after taxes. We can use this equation as an alternative way to find the answers to question 3 and 5 as follows.
3. Earn desired net income after taxes of $36,000
.9X = 180,000 + 36,000
.9X = 216,000
X = 216,000 ÷ .9 = 240,000 mixed units
5. Earn desired net income after taxes equal to 9 percent of sales dollars
.9X = 180,000 + .09(5X)
.9X = 180,000 + .45X
.45X = 180,000
X = 180,000 ÷ .45 = 400,000 mixed units
We do not covert the desired income to a before tax amount (by dividing by 1-T) because we are using the after tax version of the equation, i.e., we need NIAT in the equation, not NIBT.
SOLVING MULTIPLE PRODUCT CVP PROBLEMS IN DOLLARS
The following additional symbols are used to develop this section.
S = Total mixed sales dollars.
Si = Sales dollars for product i.
CMRi = Contribution margin ratio for product i.
M$i = The mix ratio for product i based on sales dollars. Note, these ratios are not equal to the mix ratio based on units.
WCMR = The weighted average contribution margin ratio = ∑ (CMRi)(M$i)
A summary of the cost volume profit relationships for this section is presented in Exhibit 11-4.
|
EXHIBIT 11-4 SUMMARY FOR SOLVING MULTIPLE PRODUCT CVP PROBLEMS IN DOLLARS |
||
| Number | Equation | Used to Determine |
| [1] | WCMR(S) = TFC | Sales $ at break-even point. |
| [2] | WCMR(S) = TFC + NIBT | Sales $ for target NIBT. |
| [3] | WCMR(S) = TFC + [NIAT ÷ (1-T)] | Sales $ for target NIAT. |
| [4] | WCMR(S) = TFC + (R)(S) | Sales $ for target NIBT stated as a proportion (R) of sales $. |
| [5] | WCMR(S) = TFC + [(R)(S) ÷ (1-T)] | Sales $ for target NIAT stated as a proportion (R) of sales $. |
| Si = S(M$i) | Sales dollars for each product after S is obtained. | |
BREAK-EVEN POINT IN SALES DOLLARS FOR MULTIPLE PRODUCTS
The same basic conceptual logic used in the previous sections is used to develop the equations in this section. The firm breaks even when total contribution margin is equal to total fixed costs.
[1] (WCMR)(S) = TFC
The difference between the equations for single product and multiproduct situations is that we must use a weighted average contribution margin ratio, WCMR = ∑ (CMRi)(M$I) to find the total mixed sales dollars. Then sales dollars for the individual products are found by multiplying the total mixed sales dollars (S) by the mix ratios for each product, Si = (S)(M$I)
TOTAL REVENUE NEEDED FOR TARGET NET INCOME BEFORE TAXES
Equation 2 is developed in the usual manner by simply adding the desired amount of NIBT to the right hand side of Equation 1.
[2] (WCMR)(S) = TFC + NIBT
TOTAL REVENUE NEEDED FOR TARGET NET INCOME AFTER TAXES
Revising the previous equation to include after tax profit we have:
[3] (WCMR)(S) = TFC + [NIAT ÷ (1-T)]
WHEN TARGET NET INCOME BEFORE TAXES IS STATED AS A PERCENTAGE OF SALES $
If R is used as the before tax target rate of return on sales, i.e., NIBT÷S, then the equation needed to achieve the target return before taxes is:
[4] (WCMR)(S) = TFC + (R)(S)
WHEN TARGET NET INCOME AFTER TAXES IS STATED AS A PERCENTAGE OF SALES $
If R is used as the after tax target rate of return on sales, i.e., NIAT÷S, the equation becomes,
[5] (WCMR)(S) = TFC + [(R)(S) ÷ (1-T)]
EXAMPLE 11-5
Suppose the Sandlot Cap Company information is provided to you in the following format.
| Product | Contribution Margin Ratios |
Mix Ratios Based on sales dollars |
|
X1 X2 |
.250 .375 |
.6 .4 |
TFC = $300,000.
Sandlot Cap Company management wants to know the amount of sales dollars needed for each product to accomplish the same five objectives.
1. Break even.
2. Earn desired net income before taxes of $60,000.
3. Earn desired net income after taxes of $36,000. Assume the tax rate is 40%.
4. Earn desired net income before taxes equal to 15% of sales dollars.
5. Earn a desired net income after taxes equal to 9% of sales dollars.
To find the answers we need to start by calculating the weighted average contribution margin ratio.
WCMR = (.25)(.60) + (.375)(.40) = .30
The mix ratios stated in dollars are used as the weights. Then the solutions are obtained as follows:
1. To break even. Using Equation [1] .3S = 300,000
S = 300,000 ÷ .3 = $1,000,000
S1 = (1,000,000)(.6) = $600,000
S2 = (1,000,000)(.4) = 400,000
2. To earn $60,000 before taxes. Using Equation [2] .3S = 300,000 + 60,000
S = 360,000 ÷ .3 = $1,200,000
S1 = (1,200,000)(.6) = $720,000
S2 = (1,200,000)(.4) = 480,000
3. To earn $36,000 after taxes. Using Equation [3] .3S = 300,000 + (36,000 ÷ .6)
S = 360,000 ÷.3 = $1,200,000
S1 = ($1,200,000)(.6) = $720,000
S2 = ($1,200,000)(.4) = 480,000
4. To earn desired NIBT of 15% of sales dollars. Using Equation [4]
.3S = 300,000 + .15S
.15S = 300,000
S = 300,000 ÷ .15 =
$2,000,000
S1 = ($2,000,000)(.6) = $1,200,000
S2 = ($2,000,000)(.4) = 800,000
5. To earn desired NIAT of 9% of sales dollars. Using Equation [5]
.3S = 300,000 + (.09S ÷ .6)
.15S = 300,000
S = 300,000 ÷ .15 =
$2,000,000
S1 = ($2,000,000)(.6) = $1,200,000
S2 = ($2,000,000)(.4) = 800,000
The solutions to these five questions are also illustrated in Figure 11-19 since we simply changed our emphasis from the horizontal axis (units) to the vertical axis (dollars).
The mix ratios determine whether the emphasis is on units or dollars and the manner in which the answers must be obtained. If the mix ratios are stated in units, as in Example 11-4, then the solutions must be obtained in units. If the mix ratios are stated in dollars, as in Example 11-5, then the solutions must be obtained in dollars. Why? To see why we cannot use the mix ratios interchangeably, suppose the Sandlot Cap Company data were stated in the following manner.
| Product | Price |
Variable Cost per Unit |
Mix Ratios Based on Sales Dollars |
|
X1 X2 |
$4 8 |
$3 5 |
.6 .4 |
Total fixed costs = $300,000. Now, find the break-even point in units. Try this, at least mentally before you look at the solution in the footnote below.4
Now suppose Sandlot Cap Company management gave you following information and asks for the break-even point. TFC is still $300,000. What would you do?
| Product | Contribution Margin Ratios | Mix Ratios Based on Units |
|
X1 X2 |
.25 .375 |
.75 .25 |
Think about it and then consult the footnote below.5
THE CASH FLOW BREAK-EVEN POINT
Since some of the fixed costs do not require cash payments (e.g., depreciation), the cash flow break-even point will be below the conventional accrual accounting break-even point. The following
technique is applicable:
CASH FLOW BREAK-EVEN BEFORE TAXES
The cash flow break-even point is where the cash inflows before taxes are equal to the cash outflows before taxes. This is presented in equation form below.
PX = TFC + VX - Non cash Fixed Costs
PX - VX = TFC - Non cash Fixed Costs
(P-V) X = TFC - Non cash Fixed Costs
The equation above is based on the assumption that all other costs are paid for during the period and that all sales dollars are collected during the period.
CASH FLOW BREAK-EVEN AFTER TAXES
The cash flow break-even point after taxes is where the cash inflows after taxes are equal to the cash outflows after taxes. We simply convert the contribution margin and total fixed costs to an after tax basis by multiplying by 1-T. The equation is as follows:
(1-T)(P-V)X = (1-T)(TFC) - Non cash Fixed Costs
EXAMPLE 11-6
Cal Company’s specifics from Example 11-1 are P = $10, V = $6, total fixed costs = $120,000 and the tax rate is 40%. If depreciation is $24,000 and there are no other non cash fixed costs, then the cash flow break-even point after taxes is:
(1-.4)(4X) = (1-.4)(120,000) - 24,000
2.4X = 72,000 - 24,000
X = 48,000 ÷ 2.4 = 20,000 units
The solution is verified in Exhibit 11-5 and Figure 11-20.
|
EXHIBIT 11- 5 INCOME STATEMENT SHOWING CAL COMPANY’S CASH FLOW BREAK-EVEN POINT |
|
|
Sales
(20,000)($10) Variable Costs (20,000)($6) Contribution Margin Less Total Fixed Costs Net Loss Add Tax Reduction* (.4)(40,000) Add back Depreciation** Cash Flow after taxes |
$200,000 120,000 80,000 120,000 (40,000) 16,000 24,000 0 |
* The idea is that the tax reduction can be used to reduce cash payments for taxes in some way. For example, to recalculate taxes for a prior year, or to offset taxable income in some other segment of the Company.
** Depreciation is included in the $120,000 fixed costs, but it does not require a cash outflow. Therefore it must be added back to arrive at the cash flow result.
We can also use the equation above to calculate the number of units needed to generate a desired amount of net cash inflow after taxes. Just add the desired amount and solve for X. For example, suppose management desires a net cash inflow after taxes of $36,000.
2.4X = 48,000 + 36,000
X = 84,000 ÷ 2.4 = 35,000 units
Check: (35,000units)($4) = 140,000 contribution margin. Subtract fixed cost of $120,000, then multiply by .6 and we have $12,000 NIAT. Add back depreciation of 24,000 to obtain $36,000.
THE CONTROVERSY OVER THE CONTRIBUTION MARGIN APPROACH
There are two issues that involve the contribution margin approach and the closely related direct (or variable) costing inventory valuation method. The first issue is a relatively old controversy over whether direct costing or full absorption costing is the most useful way to present accounting information.6 The second issue questions the compatibility of the contribution margin approach to activity based costing and the lean enterprise concepts of just-in-time and the theory of constraints. The second issue questions the wisdom of separating costs into fixed and variable categories.7 The following discussion concentrates on the second controversy. We will return to the first issue in the next chapter.
THE CASE AGAINST
From the activity based costing perspective, critics of the contribution margin approach argue that the costs traditionally defined as fixed costs have been increasing faster than the costs traditionally defined as variable costs. As a result, the CVP model does not reflect the cost structure of complex, multiproduct organizations. Although the CVP model may be useful for some short term forecasting and optimization decisions, it is misleading for decisions such as product introduction, product pricing, product mix and make versus buy. The so-called fixed costs are not explained by output volume, but by the diversity and complexity of the company's products, services, customers, distribution channels and product lines. The CVP approach is flawed because it assumes that the volume of production is the only cost driver. As a result, the model motivates managers to produce as much as possible to lower total unit cost8. It encourages managers to add new products and services ignoring the "overhead creep" that inevitably results.9 It supports the misguided view that the company should never drop a part of the business as long as that part generates a positive contribution margin. But this signal to constantly expand is a trap because the costs that are assumed to be constant, increase rapidly instead, in response to the greater demands that are placed on the various support activities. As the so-called fixed costs rise, the manager attempts to add more volume to lower unit cost again. The process is somewhat analogous to a dog chasing it's tail.
From the lean enterprise, or continuous improvement perspective, the contribution margin approach emphasizes maximizing output with a static set of constraints, rather than emphasizing the continuous improvement of the company’s value creating processes and activities. The contribution margin approach has the same basic defect as any other constrained optimization technique.10 It promotes short run optimization within a static system. However, from the viewpoint of the lean enterprise concepts of just-in-time and the theory of constraints, becoming competitive and maintaining competitiveness in the long run requires a dynamic learning organization. The emphasis should be on relentlessly eliminating waste, removing constraints, re-engineering processes when necessary and increasing customer value, not on maximizing output in an attempt to minimize short run unit costs.11
THE CASE FOR
Defenders of the contribution margin approach argue that the concepts of contribution margin and related techniques are useful for short term planning (Chapter 11) and for performing a variety of special relevant cost studies (Chapter 17). Although production volume is not the only cost driver, it is still the major cost driver. Production volume based systems and techniques such as direct costing and CVP analysis still provide reasonably accurate information for a fraction of the cost of elaborate ABC systems. Another advantage of these methods is that income statements based on the contribution margin approach (i.e., direct costing) are much easier for managers to understand than statements based on either traditional full absorption costing or activity based costing. (We explore this idea in the next chapter.) In addition, direct costing reduces the full cost behavioral bias towards over production by eliminating the production volume variance and the inventory change effect that increases net income when production exceeds sales.12 The contribution margin approach is neutral, or nearly neutral, because it does not encourage management to produce anything that cannot be sold. The argument that the contribution margin approach promotes overproduction is not warranted. In fact, full absorption costing creates a much stronger motivation to overproduce and ABC is just an expanded form of that same methodology. In addition, CVP analysis does not discourage continuous improvement. It is just a quantitative tool that can be used or misused like any other tool. The CVP approach can complement the plan-do-check-action (PDCA) continuous improvement cycle by providing a way to estimate the financial consequences of proposed changes in the system.
A POSSIBLE RECONCILIATION WITH ABC
A possible reconciliation between ABC and the contribution margin approach is provided by Robin Cooper's levels of cost variability.13 The idea is to combine ABC with the contribution margin approach to reveal contributions at the unit, batch, product, distribution and customer levels (See Chapter 7 to review these terms). This expanded information will indicate which products, distribution channels and customers really are profitable and perhaps help avoid the potential trap set by the contribution margin logic that keeps companies from ever dropping anything. (See the Ali summary for more on this idea).
FOOTNOTES
1 The economic, or theoretical cost-volume-profit model was developed by a number of theorist between 1800 and 1930. The classical economists (e.g., Adam Smith, David Ricardo, Thomas Malthus, Jeremy Bentham and Jean Baptiste Say) believed that the cost of production (supply) determined the market price. The marginalist (e.g., Herman Gossen, William Jevons) believed that demand was the primary determinant of market price. Around 1890, the neoclassical economist, Alfred Marshall argued that the interaction of supply and demand determines the price using his famous scissors analogy (i.e., both supply and demand are needed, just as both blades of a pair of scissors are needed to cut a piece of paper). Later, around 1930, Edward Chamberlin and others developed the theoretical model described in this chapter. Joel Dean presented the linear model as a practical alternative. See Marshall, A. 1890. Principles of Economics. The Macmillan Company; Chamberlin, E. H. 1946. The Theory of Monopolistic Competition. Harvard University Press; and Dean, J. 1951. Managerial Economics. Prentice-Hall, Inc.: 326-347; and Oser, J. 1963. The Evolution of Economic Thought. Harcourt, Brace & World, Inc. Chapter 14. (Summary).
2 See Chapter 7 (Exhibit 7-2) for some examples of non-production volume related drivers and measurements.
3 In the theoretical model, profits are maximized where marginal revenue is equal to marginal cost. Solving for this point requires using calculus. Marginal revenue is the rate of change in total revenue and can be found by taking the first derivative of the total revenue function. Marginal cost is the rate of change in total cost and can be determined by taking the first derivative of the total cost function. Upper level microeconomics textbooks show this in considerable detail using quadratic and cubic equations.
4 Although you may be tempted to multiply P-V for each product by the mix ratios to obtain the weighted average contribution margin per unit, that step will produce the wrong answer. Note that (1)(.6) + (3)(.4) = 1.8 and we know from Example 11-4 that W is 1.5 not 1.8 (See Figure 11-19). We must solve the problem in dollars first and then convert to units. Therefore, we need to calculate the contribution margin ratios (4-3)÷4 =.25 and (8-5)÷8=.375 and then solve for sales dollars as in Example 11-5, question 1 above. We calculate the weighted average contribution margin ratio, i.e., (.25)(.60) + (.375)(.4) = .30. Then solve for mixed sales dollars at the break-even point, i.e., S= $300,000 ÷ .30 = $1,000,000. Find the sales dollars for each product, S1 = (1,000,000)(.6) = $600,000 and S2 = (1,000,000).4) = $400,000. Then we divide by the sales prices to find the break-even point in units, i.e., X1 = $600,000 ÷ $4 = 150,000 caps and X2 = $400,000 ÷ $8 = 50,000 caps.
5 Multiplying the contribution margin ratios by the mix ratios and summing the results we get .28125. Comparing this number to W and WCMR (1.50 and .30 from examples 11-4 and 11-5) reveals that .28125 is not a recognizable piece of information. Any attempt to use it will produce the wrong answer. Since there is no way to find the contribution margin per unit for each product, or the mix ratios in dollars, you would need to ask for additional information to answer the question.
6 The first issue started back around 1936. See Harris, J. 1936. What did we earn last month? NACA Bulletin (January 15): 501-526. Harris used the term direct costing rather than variable costing.
7 A long list of references could be provided here, but the edited version of a 1989 panel discussion by Robert Kaplan, John Shank, Charles Horngren and Germain Boer provides the best single reference. See Robinson, M. A., editor. 1990. Journal of Management Accounting Research (Fall): 1-32. (Summary of Kaplan & Shank and Boer & Horngren).
8 This is essentially an argument that any model that recognizes the distinction between fixed and variable costs will create a bias towards overproduction. This is because total unit cost decreases as the average fixed cost per unit decreases when additional units are produced, i.e., unit fixed cost = TFC÷ X.
9 The theoretical economic model is also flawed for the same reason. Although changes in productivity are considered in the model, the problem referred to as "overhead creep" is not considered. In other words, in the theoretical model, productivity affects the rate of change in variable costs, but fixed costs remain constant.
10 The controversy over the usefulness of constrained optimization techniques is a broader issue since a long list of techniques fall into this category. The economic order quantity and economic batch size models, linear programming and standard costing provide a few examples.
11 See Johnson, H. T. 1989. Professors, customers and value: Bringing a global perspective to management accounting education. Proceedings of the Third Annual Management Accounting Symposium. American Accounting Association (Summary); and 1992, Relevance Regained: From Top-Down Control to Bottom-up Empowerment. New York: The Free Press: 44-47, and 191. (Summary).
12 These concepts are discussed in more detail in Chapters 8 and 12. The inventory change effect is also illustrated in some of the master budget problems in Chapter 9.
13 This idea was discussed by Robert Kaplan in the panel discussion referenced in footnote 7.
1. What are the assumptions underlying the conventional linear cost volume profit analysis? (See Assumptions).
2. What does a constant sales price mean? (See Figures 11-1 and 11-2). Is this realistic? (See Figures 11-3 and 11-4).
3. What does constant variable cost per unit mean? (See Figures 11-5 and 11-6).
4. What assumption causes the total variable cost function to be linear? (See Figure 11-13 for the linear functions, then Figures 11-5 and 11-6).
5. How does total variable cost and total cost change under constant, decreasing and increasing productivity? (See Figure 11-14 for the total cost functions and Figures 11-6, 11-9, and 11-7 for the underlying unit cost functions).
6. In the conventional model, how is variable cost fixed and fixed cost variable? (See Figure 11-6 for unit variable cost and draw your own graph for unit fixed costs).
7. In the microeconomic model, what causes the average variable cost curve to be U-shaped? (See Figure 11-12).
8. How do linear and non-linear CVP analysis differ in terms of in indicating how much to produce and what price to charge? (See Figures 11-15 and 11-16).
9. How is the basic break-even equation for unit data developed or derived? (See Techniques).
10. How do the five equations in Exhibit 11-1 differ?
11. What is the slope of the profit functions in Figure 11-17 and Figure 11-18?
12. Is the difference between CVP analysis in dollars and CVP analysis in units more mechanical or conceptual? Explain. (Compare Exhibits 11-2 and 11-1).
13. Theoretically, what is the maximum return on Sales $ before and after taxes, for a company that produces and sells a single product, assuming no demand or capacity constraints? (See Some Questions in Chapter 14).
14. What two weighted average calculations are needed in unit based multi-product CVP analysis? Why are they needed? (See Exhibit 11-3).
15. In multi-product CVP calculations, are the mix proportions for units and dollars the same? What are the implications? (See Note on Mix Ratios).
16. Is the cash flow break-even point in sales dollars above or below the accrual accounting break-even point? Explain why. (See Cash flow break-even and Figure 11-20).
17. What are some of the arguments against conventional linear CVP analysis? (See the Controversy of CVP).
18. Would converting to the theoretical CVP model solve the problems in question 17? (See Figure 11-16 for some ideas).
19. Is the CVP model consistent with the concept of continuous improvement? (See the Controversy of CVP).
20. Assume there are no constraints on the firm's capacity to produce or the demand for the firm's products. What would be the maximum return on sales dollars for a multi-product firm before and after taxes? (The link related to question 13 is helpful).
Some Blank Graphs useful for analysis.Max Company produces a single product that it sells wholesale for $100 per unit. Variable costs per unit amount to $80 and total fixed costs are $100,000. Assume the applicable tax rate is 40%.
Required:
a. Find the break-even point in sales dollars.
b. Find the sales dollars needed to generate $20,000 in net income before taxes.
c. Find the sales dollars needed to generate $24,000 in net income after taxes.
d. Find the sales dollars needed to generate a 9% return on sales dollars after
taxes.
e. Find the sales dollars needed to generate an 18% return on sales after taxes.
The VM Company produces and sells a line of Camcorders with a sales price and budgeted unit costs as follows:
| Sales price | $600 |
| Direct materials costs per unit | 170 |
| Direct labor costs per unit | 50 |
| Variable factory overhead per unit | 90 |
| Total fixed factory overhead | 400,000 |
| Variable Selling & Adm costs per unit sold | 30 |
| Total Fixed Selling & Adm costs | 120,000 |
Required:
1. Determine VM Company's conventional linear break-even point in units.
2. Assume a tax rate of forty percent. Using conventional linear cost volume profit analysis, determine the number of units that VM Company would have to produce and sell to generate net income of $78,000 after taxes.
3. Now suppose the company wants to earn 10% on sales revenue after taxes. Using conventional linear cost volume profit analysis, determine the number of units VM would need to be produce and sell to accomplish this goal?
PROBLEM 11-3The ESP Company produces two types of t-shirts, front design and wraparound design. For convenience we will call them products A and B. The company’s wholesale prices and relevant costs appear below:
| Product | A | B |
| Sales
Price Direct material Direct labor Variable overhead Manufacturing margin Variable Selling & Adm. costs Contribution margin |
$2.00 .50 .10 .40 1.00 .60 .40 |
$4.00 1.00 .20 .80 2.00 1.00 1.00 |
Total Fixed Costs:
Manufacturing $34,000
Selling & Adm. 10,000
The budgeted sales mix in units is 80% product B and 20% product A.
Required:
a. Find the break-even point in units of A and B based on the budgeted sales mix.
b. Assume a tax rate of 40%. What is the maximum return on sales dollars the firm could earn assuming no capacity or demand constraints?
c. How many units of A and B would the firm need to produce and sell to earn budgeted net income of $79,200 after taxes?
d. How many units of A and B would the firm need to produce and sell to earn an 11% budgeted return on sales dollars after taxes.
PROBLEM 11-4The Gong Company produces and sells three types of jigsaws, variable speed (A), single speed (B) and variable speed with auto-scrolling (C). Budgeted data is given below:
| Product | Sales Price | Variable cost Per Unit | Sales Mix as a Proportion
of Total Sales $ |
| A B C |
$30 20 40 |
$15 12 30 |
.10 .50 .40 |
Budgeted total fixed costs are $700,000.
Required:
a. Calculate the break-even point in sales dollars for each product based on the budgeted sales mix.
b. Determine the sales dollars of each product needed to generate a budgeted after tax profit of $245,000. Assume a 50% tax rate.
c. Determine the sales dollars of each product needed to generate a 15% budgeted return on sales dollars after taxes.
PROBLEM 11-5US Electric Company produces a line of color TV sets with the following budgeted sales prices, unit variable costs, and sales mix ratios.
| Product | Unit Sales Price |
Unit Variable Cost |
Budgeted Mix Ratios Based on Units |
| 1 | $100 | $60 | .10 |
| 2 | 120 | 72 | .12 |
| 3 | 140 | 77 | .12 |
| 4 | 160 | 88 | .14 |
| 5 | 180 | 90 | .16 |
| 6 | 200 | 100 | .12 |
| 7 | 240 | 108 | .08 |
| 8 | 280 | 126 | .08 |
| 9 | 320 | 128 | .04 |
| 10 | 360 | 144 | .04 |
Required:
1. Total fixed costs equal $2,335,000, and the tax rate is 40%. Use the computer program to determine the budgeted unit sales for each product needed to generate a desired net income after taxes equal to 15% of sales dollars.
2. Solve this problem by hand to verify your computer solution.
3. Suppose the mix ratios for products 5 and 10 were reversed, i.e., .04 for product 5 and .16 for product 10.
a. Would total sales dollars required in question 1 increase or decrease? Why?
b. Would net income increase or decrease?
c. Would the total number of units increase or decrease?
d. What would happen to the break-even point?
PROBLEM 11-6The Tampa Company produces two types of exercise machines, Pumpup (X1) and Treadmill (X2). Relevant data are as follows:
| Product | Contribution Margin Per Unit |
Budgeted Sales Mix in Units |
| X1 X2 |
$100 200 |
60% 40% |
The company’s total fixed costs amount to $350,000 which represents $200,000 fixed manufacturing overhead and $150,000 fixed selling and administrative expenses.
Required:
a. Determine the number of units of each product the company needs to produce and sell to break-even.
b. Determine the number of units of each product needed to generate net income after taxes equal to $96,250. Assume a tax rate of 45%.
The St. Pete Company produces two types of tape rulers, a 25 foot (A1) and a 50 foot (A2). Prices, costs and mix ratios are as follows:
| Product | Sales Price | Variable Cost Per Unit |
Budgeted Sales Mix in Dollars |
| A1 A2 |
$10 4 |
$6.50 2.80 |
20% 80% |
Total fixed costs amount to $62,000 and the tax rate is 45%.
Required:
a. Find the break-even point in dollars of A1 and A2.
b. If St. Pete Company purchased a piece of equipment that added an additional $4,000 to fixed costs, how many units of each product would be needed to generate an 11% return on sales revenue after taxes?
PROBLEM 11-8The York Company produces Dirt bikes (Y1) and Road bikes (Y2) as follows:
| Product | Sales Price | Variable Cost Per Unit |
Budgeted Mix in Units |
| Y1 Y2 |
$200 400 |
$80 160 |
80% 20% |
Total fixed costs amount to $388,800 which represents $238,800 fixed manufacturing overhead and $150,000 fixed selling and administrative expenses.
Required:
a. Determine the number of units of each product the company needs to produce and sell to break-even, assuming that unit sales are in proportion to the budgeted mix.
b. Determine the number of units of each product needed to generate net income after taxes equal to $72,000. Assume a tax rate of 40 percent, and sales are in proportion to the budgeted mix.
c. Determine the number of units of each product needed to generate a 20% return on sales dollars after taxes. Again assume a tax rate of 40 percent and that sales are in proportion to the budgeted mix.
PROBLEM 11-9Zippo Company produces two hand held video games named Crazy Monkey (X1) and Power Pig (X2). The games have the following cost and selling prices.
| Product | X1 | X1 |
| Sales Price | $10 | $12 |
| Variable Manufacturing Costs | 4 | 3 |
| Manufacturing Margin | 6 | 9 |
| Variable Selling & Adm. Costs | 2 | 2 |
| Contribution Margin | 4 | 7 |
Total Fixed Costs:
Manufacturing $200,000.
Selling & Administrative 58,000.
The budgeted sales mix is based on past experience which indicates that the company typically sells twice as many X1's as it does X2's. For some reason, Crazy Monkeys are twice as popular as Power Pigs.
REQUIRED:
a. Determine the number of units of each product the firm would need to produce and sell to break-even based on the budgeted sales mix.
b. Determine the number of units of each product the firm would need to produce and sell to generate budgeted net income after taxes equal to 12 percent of budgeted sales dollars. Assume the tax rate is 40%.
c. Assume that the non-cash fixed costs (i.e., costs that do not require a cash payment) are $55,800. Find the cash flow break-even point in units of X1 and X2.