Summary by Cathy Riemer
Master of Accountancy Program
University of South Florida, Summer 2002
Quality Related Main Page |
Deming Main Page
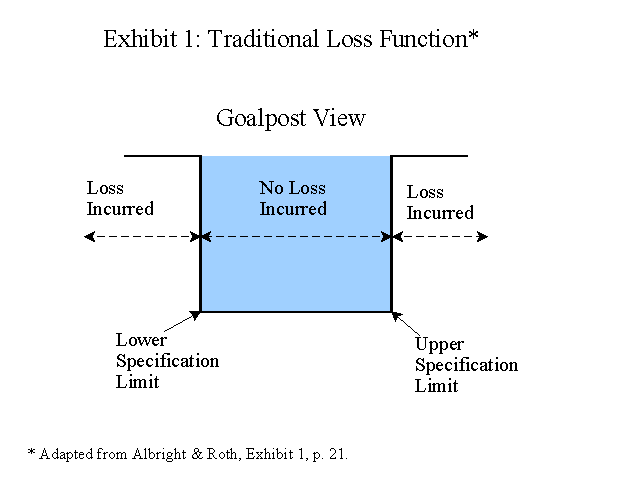
The Goalpost (Traditional) View of Quality
Traditionally, companies measure quality by the number of defects or the defect rate. In this system, defects are identified through inspections of the materials and products. Upper and lower quality limits are established. Everything that does not fall within the limits is considered a defect.
This view is referred too as the goalpost view because it can be conformed to the use of goalposts in football. If the extra point goes between the goal posts it is considered a success. It does not matter whether or not it is in the center or close to the sides. However, if the ball goes wide, left or right, it is unsuccessful. Exhibit 1 shows this view.

The Quality Loss Function (QLF)
The quality loss function is based on the work of electrical engineer, Genichi Taguchi. This view disagrees with the traditional (goalpost) view. The quality loss function recognizes that products falling between specific limits are not all equal. The four following statements summarize Taguchi’s philosophy.
1. We cannot reduce cost without affecting quality.
2. We can improve quality without increasing cost.
3. We can reduce cost by improving quality.
4. We can reduce cost by reducing variation. When we do so, performance and quality will automatically improve.
In Taguchi’s view, quality is not defined by specific limits, but rather on whether or not it creates a financial loss to society. An example given is a defective automobile exhaust system creating air pollution.
There are many types of quality loss functions. However, in all types, the loss is determined by evaluating variation from a specific target. Taguchi’s philosophy includes three general ways to evaluate the relationship between quality and variability.
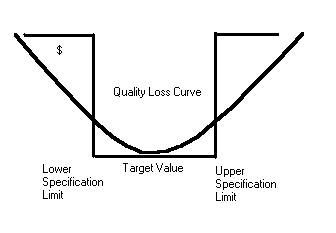
Nominal is better approach
In this approach, the closer to the target value, the better. It does not matter whether the deviation is above or below the target value. Under this approach the deviation is quadratic. The following exhibit portrays the nominal is better approach.
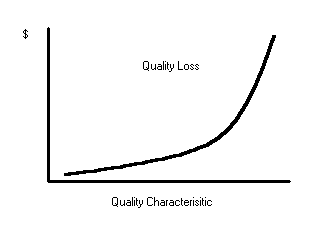
Smaller is better approach
The smaller is better approach is when a company desires smaller values. As the value gets larger, the loss incurred grows. The following exhibit portrays the smaller is better approach.
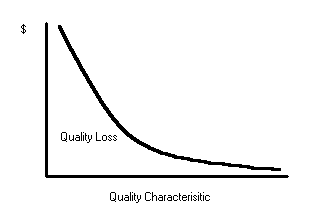
Larger is better approach
Larger is better occurs when a company desires higher values of a characteristic. Two examples given are employee participation and the customer acceptance rate. Under this approach, the larger the characteristic, the smaller the quality loss function. The following exhibit portrays the larger is better approach.
Uses of Quality Loss Function (QLF) Data
1. Reduces Costs
There are three ways that managers can use QLF to reduce costs.
1. Move the average of the actual distribution closer to
the target value.
2. Reduce variability.
3. Do a combination of both.
2. Setting Specific Limits
The data from the quality loss function can be used to determine where limits should be set to help minimize losses.
Sony Corporation Example
Sony uses the Taguchi model in managing the television sets it produces. The quality characteristic is the color density of the televisions. The Sony engineers set specific limits for color density at a plus or minus tolerance level. One of Sony’s plants uniformly distributed televisions that fell between the specification limits. The other plant followed a normal distribution with an average near the set target.
A comparison of customer responses shows that a higher level of satisfaction was reported on televisions from the second plant. Also, the second plant’s warranty expenses were lower.
This case shows the problem with focusing on a defect rate rather than a variation from the target. The first plant shipped at a zero defect rate, however, the specification limits allowed for too much variation. In the second plant, the limits were smaller and the quality was more consistent. The Taguchi model provides a good way to analyze the costs associated with variability, even within the limits.
In conclusion, if companies want to remain competitive, they have to provide quality products. To accomplish this, a company must focus on the reduction of variability of a product’s characteristics around a specific target value. The traditional approach is not enough. To remain a world competitor, a company must consider the Taguchi QLF approach.
___________________________________________
Related summaries:
Albright, T. L. and H. Roth. 1992. The measurement of quality costs: An alternative paradigm. Accounting Horizons (June): 15-27. (Summary).
Anderson, S. W. and K. Sedatole. 1998. Designing quality into products: The use of accounting data in new product development. Accounting Horizons (September): 213-233. (Summary).
Deming, W. E. 1993. The New Economics for Industry For Industry, Government & Education. Cambridge: Massachusetts Institute of Technology Center for Advanced Engineering Study. Chapter 10. (Summary).
Kim, M. W. and W. M. Liao. 1994. Estimating hidden quality costs with quality loss functions. Accounting Horizons (March): 8-18. (Summary).
Martin, J. R. Not dated. Constrained optimization techniques. Management And Accounting Web. ConstrainoptTechs.htm
Martin, J. R. Not dated. Summary of the 1992 PBS Program Quality or Else. Management And Accounting Web. QualityOrElse.htm
Martin, J. R. Not dated. What is Six Sigma? Management And Accounting Web. SixSigmaSummary.htm
Roth, H. P. and T. L. Albright. 1994. What are the costs of variability? Management Accounting (June): 51- 55. (Summary).
Sedatole, K. L. 2003. The effect of measurement alternatives on a nonfinancial quality measure's forward-looking properties. The Accounting Review (April): 555-580. (Summary).
Taguchi, G. and D. Clausing. 1990. Robust quality. Harvard Business Review (Jan-Feb): 65-75. (Summary).